题目内容
如图，一个牧童在小河的南4km的A处牧马，而他正位于他的小屋B的西8km北7km处，他想把他的马牵到小河边去饮水，然后回家．他要完成这件事情所走的最短路程是多少？
分析：构建直角三角形，利用勾股定理即可得．
解答：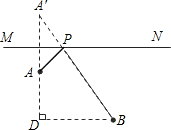
解：如图，作出A点关于MN的对称点A′，连接A′B交MN于点P，
则A′B就是最短路线．
在Rt△A′DB中，由勾股定理求得
A′B=
=
=17km．
答：他要完成这件事情所走的最短路程是17km．
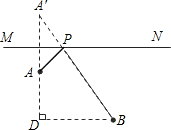解：如图，作出A点关于MN的对称点A′，连接A′B交MN于点P，则A′B就是最短路线．
在Rt△A′DB中，由勾股定理求得
A′B=
| (DA′)2+DB2 |
| (7+4+4)2+82 |
答：他要完成这件事情所走的最短路程是17km．
点评：本题考查的是勾股定理在实际生活中的运用，需要同学们联系实际，熟练掌握．
练习册系列答案
相关题目
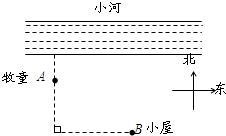25、如图，一个牧童在小河的南4km的A处牧马，而他正位于他的小屋B的西8km北7km处，他想把他的马牵到小河边去饮水，然后回家．
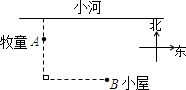如图，一个牧童在小河的南4km的A处牧马，而他正位于他的小屋B的西8km北7km处，他想把他的马牵到小河边去饮水，然后回家．他要完成这件事情所走的最短路程是（ ）
