题目内容
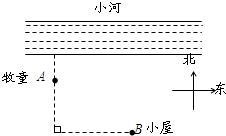 25、如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.
25、如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.(1)马牵到小河边什么地方饮水,然后回家所走的路程最短?请在图中画出河边马饮水的位置;
(2)如果牧童牵马行走的速度为每小时5km,为了尽早回家,请求出他在A处牵马到小河边去饮水,然后回家所需最短时间.
分析:(1)本题要在河边找一点D,使AD+BD最小.可作出点A关于河的对称点A′,连接A′B,交河岸于点D,则点D是马饮水的位置.(2)由勾股定理求解.
解答: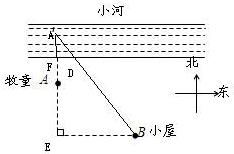 解:(1)如图,作出点A关于河的对称点A′,连接A′B,交河岸于点D,则点D是马饮水的位置.
解:(1)如图,作出点A关于河的对称点A′,连接A′B,交河岸于点D,则点D是马饮水的位置.
(2)由题意知,AA′=8,AE=7,BE=8,
由勾股定理知,A′B=17.
∴回家所需最短时间t=17÷5=3.4小时.
 解:(1)如图,作出点A关于河的对称点A′,连接A′B,交河岸于点D,则点D是马饮水的位置.
解:(1)如图,作出点A关于河的对称点A′,连接A′B,交河岸于点D,则点D是马饮水的位置.(2)由题意知,AA′=8,AE=7,BE=8,
由勾股定理知,A′B=17.
∴回家所需最短时间t=17÷5=3.4小时.
点评:本题利用了轴对称及两点之间线段最短的性质,并运用了勾股定理求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?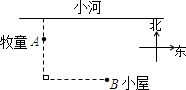 如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是( )
如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是( )

