题目内容
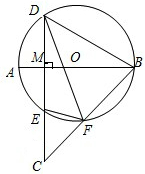已知：如图，在⊙O中，AB是直径，CD⊥AB于M，交⊙O于E，连接CB交⊙O于F，求证：EF•DF=BF•CF．
分析：根据垂径定理可以发现等弧，根据等弧所对的圆周角相等可以证明角相等．即∠BFD=∠BDC．再加上公共角，则可以发现△BDF∽△BCD；根据圆内接四边形的外角等于它的内对角，可以得到∠EFC=∠BDC，再加上公共角，可以证明△BDC∽△EFC．从而借助中间比
，证明结论．
| BD |
| CD |
解答：证明：∵AB是⊙O的直径，DC⊥AB，
∴弧BD=弧BE，∠BDC=∠BFD．
∵∠DBF=∠CBD，
∴△BDF∽△BCD．
∴
=
．
∵∠EFC=∠BDC，∠C=∠C，
∴△BDC∽△EFC．
∴
=
∴
=
．
∴EF•DF=BF•CF．
∴弧BD=弧BE，∠BDC=∠BFD．
∵∠DBF=∠CBD，
∴△BDF∽△BCD．
∴
| BF |
| DF |
| BD |
| DC |
∵∠EFC=∠BDC，∠C=∠C，
∴△BDC∽△EFC．
∴
| BD |
| DC |
| EF |
| FC |
| BF |
| DF |
| EF |
| FC |
∴EF•DF=BF•CF．
点评：能够充分运用垂径定理和圆周角定理以及圆内接四边形的性质发现圆中的角相等；掌握相似三角形的判定和性质．能够借助中间比证明一个比例式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
24、已知：如图，在?ABCD中，对角线AC交BD于点O，四边形AODE是平行四边形．求证：四边形ABOE、四边形DCOE都是平行四边形．
21、已知：如图，在△ABC中，AB=AC，点D，E在边BC上，且BD=CE．
（1）计算：
点A重合．将线段AP绕点A逆时针旋转到AQ，使∠PAQ=∠BAC，连接BP，CQ
（2012•密云县一模）已知：如图，在△ABC中，∠A=∠B=30°，D是AB 边上一点，以AD为直径作⊙O恰过点C．