Question

【题目】如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S1 ， S2 ， 则S1+S2的值为

Answer 1

【答案】17
【解析】解：如图，
设正方形S1的边长为x，
∵△ABC和△CDE都为等腰直角三角形，
∴AB=BC，DE=DC，∠ABC=∠D=90°，
∴sin∠CAB=sin45°= = ，即AC= BC，同理可得：BC=CE= CD，
∴AC= BC=2CD，又AD=AC+CD=6，
∴CD= =2，
∴EC2=22+22 ， 即EC=2 ；
∴S1的面积为EC2=2 ×2 =8；
∵∠MAO=∠MOA=45°，
∴AM=MO，
∵MO=MN，
∴AM=MN，
∴M为AN的中点，
∴S2的边长为3，
∴S2的面积为3×3=9，
∴S1+S2=8+9=17．
所以答案是：17．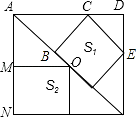

【考点精析】通过灵活运用正方形的性质和相似三角形的判定与性质，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方即可以解答此题．