题目内容
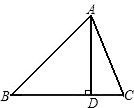 已知:如图,AD是△ABC的高,∠BAD=45°,AC=13cm,CD=5cm,则AD=
已知:如图,AD是△ABC的高,∠BAD=45°,AC=13cm,CD=5cm,则AD=分析:在Rt△ACD中,已知AC,CD的长,根据勾股定理可求得AD的长,再根据等腰三角形的性质可得到BD的长,最后根据三角形的面积公式即可求解.
解答:解:∵AD是△ABC的高,AC=13cm,CD=5cm
∴AD=12cm
∵AD是△ABC的高,∠BAD=45°
∴AD=BD=12cm
∴BC=BD+CD=12+5=17cm
∴S△ABC=
×BC×AD=102cm2
∴AD=12cm
∵AD是△ABC的高,∠BAD=45°
∴AD=BD=12cm
∴BC=BD+CD=12+5=17cm
∴S△ABC=
| 1 |
| 2 |
点评:此题主要考查学生对勾股定理及等腰三角形的性质等知识点的运用能力.

练习册系列答案
相关题目
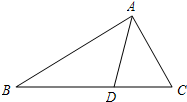 已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )
已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )| A、3:2 | B、9:4 | C、2:3 | D、4:9 |
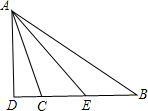 已知:如图,AD是△ABC的高,试判断∠DAE与∠B、∠ACB之间的关系,并说明理由.
已知:如图,AD是△ABC的高,试判断∠DAE与∠B、∠ACB之间的关系,并说明理由.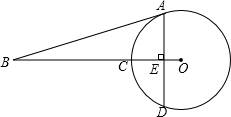
 已知:如图,AD是一条直线,∠1=65°,∠2=115°.求证:BE∥CF.
已知:如图,AD是一条直线,∠1=65°,∠2=115°.求证:BE∥CF. 已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.求证:GE∥AD.
已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.求证:GE∥AD.