题目内容
已知:如图,AD是⊙O的弦,OB⊥AD于点E,交⊙O于点C,OE=1,BE=8,AE:AB=1:3.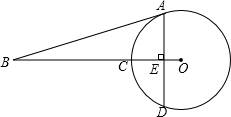
(1)求证:AB是⊙O的切线;
(2)点F是弧ACD上的一点,当∠AOF=2∠B时,求AF的长.
分析:(1)先连接OA,由AE:AB=1:3,设AE=x,则AB=3x.根据OB⊥AD于E,BE=8,利用勾股定理求出AE的长、AB的长,再在Rt△AEO中,根据勾股定理求出AO的长,又因为AB2+OA2=81,OB2=81,所以OB2=AB2+OA2.从而证得△OAB是直角三角形.所以OA⊥AB.从而证得AB是⊙O的切线.
(2)作直径AM,连接DM,得到∠DOM=2∠OAE,再由∠B=∠OAE,得到∠DOM=2∠B.由点O是AM的中点,点E是AD的中点,OE=1,得到DM=2OE=2.再将△ODM绕点O顺时针方向旋转,得到∠AOF=∠DOM=2∠B,当点D与点A重合时,点M与点F重合.从而求得AF=DM=2.
(2)作直径AM,连接DM,得到∠DOM=2∠OAE,再由∠B=∠OAE,得到∠DOM=2∠B.由点O是AM的中点,点E是AD的中点,OE=1,得到DM=2OE=2.再将△ODM绕点O顺时针方向旋转,得到∠AOF=∠DOM=2∠B,当点D与点A重合时,点M与点F重合.从而求得AF=DM=2.
解答: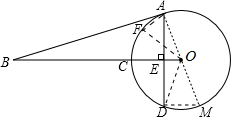 (1)证明:连接OA.
(1)证明:连接OA.
∵AE:AB=1:3,
∴设AE=x,则AB=3x.
∵OB⊥AD于E,BE=8,
∴(3x)2=x2+82.
解得x=2
(舍负).
∴AE=2
,AB=6
.
∵OE=1,
∴AO=
=3.
∵AB2+OA2=81,OB2=81,
∴OB2=AB2+OA2.
∴△OAB是直角三角形.
∴OA⊥AB.
∴AB是⊙O的切线.
(2)解:作直径AM,连接DM.
∴∠DOM=2∠OAE.
∵∠B=∠OAE,
∴∠DOM=2∠B.
∵点O是AM的中点,点E是AD的中点,OE=1,
∴DM=2OE=2.
将△ODM绕点O顺时针方向旋转,
∵∠AOF=∠DOM=2∠B,
∴当点D与点A重合时,点M与点F重合.
∴AF=DM=2.
 (1)证明:连接OA.
(1)证明:连接OA.∵AE:AB=1:3,
∴设AE=x,则AB=3x.
∵OB⊥AD于E,BE=8,
∴(3x)2=x2+82.
解得x=2
| 2 |
∴AE=2
| 2 |
| 2 |
∵OE=1,
∴AO=
| AE2+OE2 |
∵AB2+OA2=81,OB2=81,
∴OB2=AB2+OA2.
∴△OAB是直角三角形.
∴OA⊥AB.
∴AB是⊙O的切线.
(2)解:作直径AM,连接DM.
∴∠DOM=2∠OAE.
∵∠B=∠OAE,
∴∠DOM=2∠B.
∵点O是AM的中点,点E是AD的中点,OE=1,
∴DM=2OE=2.
将△ODM绕点O顺时针方向旋转,
∵∠AOF=∠DOM=2∠B,
∴当点D与点A重合时,点M与点F重合.
∴AF=DM=2.
点评:本题考查了切线的判断与性质、勾股定理以及垂径定理,此题综合性较强,难度适中,有利于学生能力提高.

练习册系列答案
相关题目
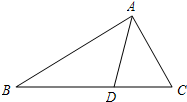 已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )
已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )| A、3:2 | B、9:4 | C、2:3 | D、4:9 |
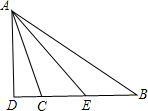 已知:如图,AD是△ABC的高,试判断∠DAE与∠B、∠ACB之间的关系,并说明理由.
已知:如图,AD是△ABC的高,试判断∠DAE与∠B、∠ACB之间的关系,并说明理由. 已知:如图,AD是一条直线,∠1=65°,∠2=115°.求证:BE∥CF.
已知:如图,AD是一条直线,∠1=65°,∠2=115°.求证:BE∥CF. 已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.求证:GE∥AD.
已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.求证:GE∥AD.