��Ŀ����
����Ŀ������ABC�У�AB=20cm��BC=16cm����DΪ�߶�AB���е㣬����P��2cm/s���ٶȴ�B�����������BC���˶���ͬʱ��Q��a cm/s��a��0��a��2�����ٶȴ�C��������߶�CA���˶������˶�ʱ��Ϊx�룮
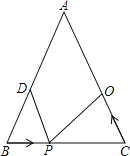
��1����AB=AC��P���߶�BC�ϣ���aΪ��ֵʱ���ܹ�ʹ��BPD����CQPȫ�ȣ�
��2������B=60����������������BDPΪֱ�������Σ�
��3������C=70��������CPQ�Ķ���Ϊ����ʱ����CPQΪ���������Σ�����ֱ��д���𰸣�����д�����̣���
���𰸡���1��![]() cm/s����2����P����2.5���10�����BPDΪֱ�������Σ���3������CPQΪ����������ʱ����CPQ�Ķ���Ϊ35�㣬40�㣬55�㣬70�㣮
cm/s����2����P����2.5���10�����BPDΪֱ�������Σ���3������CPQΪ����������ʱ����CPQ�Ķ���Ϊ35�㣬40�㣬55�㣬70�㣮
��������
�����������1������ȫ��������Ӧ���������̽���֮��Ĺ�ϵ���ٸ���·��=�ٶȡ�ʱ�乫ʽ������õ�P�˶���ʱ�䣬����õ�Q���˶��ٶȣ�
��2��������������ٵ���BPD=90��ʱ������B=60�����õ���BDP=30�������2BP=BD=10�����x=2.5���ڵ���BDP=90��ʱ�����������ε��ڽǺ͵õ���BPD=30�������x=10�����ɵõ���P����2.5���10�����BPDΪֱ�������Σ�
��3���ֵ�P�ڱ�BC�ϻ��P�ڱ�BC���ӳ����ϣ���CPQΪ���������Σ����ݵ��������ε����ʺ������ε��ڽǺͼ��ɵõ����ۣ�
�⣺��1����AB=AC��
���B=��C��
��AB=20cm��D��AB���е㣬
��BD=10cm��
����Q���ٶ����P���ٶȲ�ͬ��
��BP��CQ��
Ҫʹ��BPD����CQPȫ�ȣ�
��BP=CP=8cm CQ=BD=10cm��
��x=![]() �룬
�룬
��a=![]() =
=![]() cm/s��
cm/s��
��2���ٵ���BPD=90��ʱ��
�ߡ�B=60�������BDP=30����
��2BP=BD=10��
��BP=5��
��2x=5��
��x=2.5��
�ڵ���BDP=90��ʱ��
�ߡ�B=60����
���BPD=30����
��BP=2BD=20��
��2x=20��
��x=10��
����P����2.5���10�����BPDΪֱ�������Σ�
��3����P�ڱ�BC�ϣ���CPQΪ���������Σ�
�ٵ�PQ=CQ���ߡ�C=70����
���CPQ=��C=70����
�ڵ�PQ=PC���ߡ�C=70����
���PQC=��C=70����
���CPQ=180����2��70��=40�㣬
�۵�PC=CQ���ߡ�C=70����
���CPQ=��CQP=![]() =55�㣬
=55�㣬
��P�ڱ�BC���ӳ����ϣ���CPQΪ���������Σ�
�ߡ�ACB=70�������ACP=110����
��PC=CQ��
���CPQ=��CQP=![]() =35�㣬
=35�㣬
��������������CPQΪ����������ʱ����CPQ�Ķ���Ϊ35�㣬40�㣬55�㣬70�㣮

 ��У����ϵ�д�
��У����ϵ�д�