Question

【题目】如图，已知直线y=kx-6与抛物线y=ax2+bx+c相交于A，B两点，且点

A（1，-4）为抛物线的顶点，点B在x轴上．直线AB交y轴于点D,抛物线交y轴于点C．

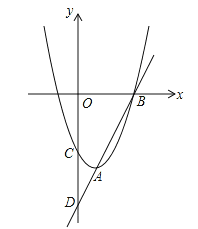
（1）求直线AB的解析式；

（2）求抛物线的解析式；

（3）在y轴上是否存在点Q，使△ABQ为直角三角形？若存在，请求出点Q的坐标；若不存在，请说明理由。

Answer 1

【答案】（1）y=2x-6，（2）y=x2-2x-3；（3）（0，-）或（0，）或（0，-1）或（0，-3）．

【解析】

试题分析：（1）把点A坐标代入y=kx-6，根据待定系数法即可求得直线AB的解析式；

（2）根据直线AB的解析式求出点B的坐标，点A是抛物线的顶点，那么可以将抛物线的解析式设为顶点式，再代入点B的坐标，依据待定系数法即可求解；

（3）分别以A、B、Q为直角顶点，分类进行讨论．找出相关的相似三角形，依据对应线段成比例进行求解即可．

试题解析：（1）把A（1，-4）代入y=kx-6，得k=2，

∴直线AB的解析式为y=2x-6，

（2）∵抛物线的顶点为A（1，-4），

∴设此抛物线的解析式为y=a（x-1）2-4，

∵点B在直线y=2x-6上，且横坐标为0，

∴点B的坐标为（3，0），

又∵点B在抛物线y=a（x-1）2-4上，

∴a（3-1）2-4=0，解之得a=1，

∴此抛物线的解析式为y=（x-1）2-4，即y=x2-2x-3；

（3）在y轴上存在点Q，使△ABQ为直角三角形．理由如下：

作AE⊥y轴，垂足为点E．

又∵点D是直线y=2x-6与y轴的交点，点C是抛物线y=x2-2x-3与y轴的交点

∴E（0，-4），D（0，-6），C（0，-3）

∴OD=6，OE=4，AE=1，ED=2，OC=3，OB=3，BD=，AD=

①如图，当∠Q1AB=90°时，△DAQ1∽△DOB，

∴，即，

∴DQ1=，

∴OQ1=6-=，即Q1（0，-）；

②如图，当∠Q2BA=90°时，△BOQ2∽△DOB，

∴，即，

∴OQ2=，即Q2（0，）；

③如图，当∠AQ3B=90°时，则△BOQ3∽△Q3EA，

∴，即，

∴OQ32-4OQ3+3=0，

∴OQ3=1或3，

即Q3（0，-1），Q4（0，-3）．

综上，Q点坐标为（0，-）或（0，）或（0，-1）或（0，-3）．