题目内容
 如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F.
如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F.
(1)求证:PC2=PE•PF;
(2)若菱形边长为8,PE=2,EF=6,求FB的长.
(1)证明:
法1:∵四边形ABCD是菱形,∴DC=DA,∠ADP=∠CDP,DC∥AB,
又∵DP是公共边,∴△DAP≌△DCP,
∴PA=PC,∠DAP=∠DCP,
由DC∥FA得,∠F=∠DCP,
∴∠F=∠DAP,又∵∠EPA=∠APF
∴△AEP∽△FAP,
∴PA2=PE•PF
∴PC2=PE•PF.
法2:∵四边形ABCD是菱形
∴DC∥AB,AD∥BC
∴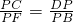 ,
,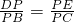
∴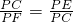
∴PC2=PE•PF.
(2)解:∵PE=2,EF=6,∴PF=8,
∵PC2=PE•PF,∴PC2=16∴PC=4,
∵DC∥FB
∴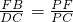 ,
,
又DC=8,∴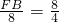
∴FB=16.
分析:(1)可由相似三角形△AEP∽△FAP对应边成比例进行求解,也可由平行线分线段成比例定理进行求解,两者均可;
(2)由题中已知线段的长度,结合(1)中的结论,再由平行线分线段成比例,即可得出结论.
点评:本题主要考查了全等三角形的判定及性质以及菱形的性质和相似三角形的判定及性质问题,能够熟练掌握.
法1:∵四边形ABCD是菱形,∴DC=DA,∠ADP=∠CDP,DC∥AB,
又∵DP是公共边,∴△DAP≌△DCP,
∴PA=PC,∠DAP=∠DCP,
由DC∥FA得,∠F=∠DCP,
∴∠F=∠DAP,又∵∠EPA=∠APF
∴△AEP∽△FAP,
∴PA2=PE•PF
∴PC2=PE•PF.
法2:∵四边形ABCD是菱形
∴DC∥AB,AD∥BC
∴
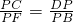 ,
,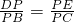
∴
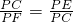
∴PC2=PE•PF.
(2)解:∵PE=2,EF=6,∴PF=8,
∵PC2=PE•PF,∴PC2=16∴PC=4,
∵DC∥FB
∴
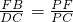 ,
,又DC=8,∴
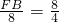
∴FB=16.
分析:(1)可由相似三角形△AEP∽△FAP对应边成比例进行求解,也可由平行线分线段成比例定理进行求解,两者均可;
(2)由题中已知线段的长度,结合(1)中的结论,再由平行线分线段成比例,即可得出结论.
点评:本题主要考查了全等三角形的判定及性质以及菱形的性质和相似三角形的判定及性质问题,能够熟练掌握.

练习册系列答案
相关题目
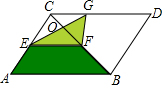 如图,点F是菱形ABDC对角线BC上一动点,EF∥AB,GF∥AC,菱形两条对角线BC和AD的长分别为2cm、5cm,当点F在BC上移动时,阴影面积会改变吗?如果不变,请求出阴影部分的面积.
如图,点F是菱形ABDC对角线BC上一动点,EF∥AB,GF∥AC,菱形两条对角线BC和AD的长分别为2cm、5cm,当点F在BC上移动时,阴影面积会改变吗?如果不变,请求出阴影部分的面积.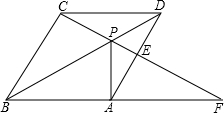 长线于F.
长线于F. (2013•苏州)如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长交边AD于点F,交CD的延长线于点G.
(2013•苏州)如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长交边AD于点F,交CD的延长线于点G.
