题目内容
如图,点P是菱形ABCD对角线BD上一点,连接CP并延长交AD于点E,交BA的延长线于点F.

(1)求证:∠DCP=∠DAP;
(2)若AB=2,DP∶PB=1∶2,且PA⊥BF,求对角线BD的长.
【答案】
(1)证明DCP≌△DAP得∠DCP=∠DAP(2)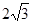
【解析】
试题分析:(1)证明:∵四边形ABCD是菱形,
∴∠ADB=∠CDB,AD=DC
∵DP=DP
∴△DCP≌△DAP
∴∠DCP=∠DAP
(2)∵ 四边形ABCD是菱形
∴AB=AD=DC=2,AB∥CD
∴ ,∠CDB=∠DBA
,∠CDB=∠DBA
∴AD=AB=AF=2
∴∠ADF=90°,∠DBP=∠ADB
∴∠DFB+∠DBF=90°
∵PA⊥BF,∴∠DAF+∠DAP=90°
∴∠DAF=∠DFA
∴AD=DF=2
∴BD= =
=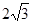
考点:三角形全等、勾股定理
点评:本题考查三角形全等、勾股定理,掌握勾股定理的内容,会判定两个三角形全等

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
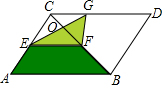 如图,点F是菱形ABDC对角线BC上一动点,EF∥AB,GF∥AC,菱形两条对角线BC和AD的长分别为2cm、5cm,当点F在BC上移动时,阴影面积会改变吗?如果不变,请求出阴影部分的面积.
如图,点F是菱形ABDC对角线BC上一动点,EF∥AB,GF∥AC,菱形两条对角线BC和AD的长分别为2cm、5cm,当点F在BC上移动时,阴影面积会改变吗?如果不变,请求出阴影部分的面积.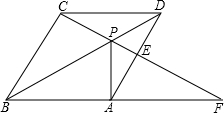 长线于F.
长线于F. (2013•苏州)如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长交边AD于点F,交CD的延长线于点G.
(2013•苏州)如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长交边AD于点F,交CD的延长线于点G.