题目内容
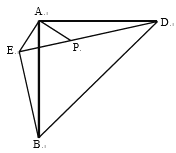
【题目】如图，矩形
在平面直角坐标系内，其中点
，点
，点
和点
分别位于线段
，
上，将
沿
对折，恰好能使点
与点
重合．若
轴上有一点
，能使
为等腰三角形，则点的坐标为___________．
【答案】
或
【解析】
首先根据矩形和对折的性质得出AC、AB、BC、AD，然后利用△ADE∽△ABC，得出AE，分类讨论即可得出点P坐标.
∵矩形
，
，
∴OA=BC=2，OC=AB=4
∴
由对折的性质，得△ADE是直角三角形，AD=CD=
AC=
，∠ADE=∠ABC=90°，∠DAE=∠BAC
∴△ADE∽△ABC
∴
，即
∴
∵
轴上有一点
，使
为等腰三角形，
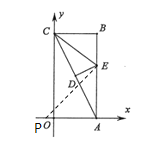
当点P在点A左侧时，如图所示：
∴
∴点P坐标为；
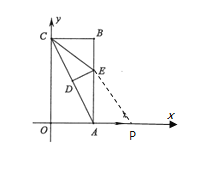
当点P在点A右侧时，如图所示：
∴
∴点P坐标为；
综上，点P的坐标是或
故答案为：或.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】郑州市自2019年12月1日起推行垃圾分类，广大市民对垃圾桶的需求剧增．为满足市场需求，某超市花了7900元购进大小不同的两种垃圾桶共800个，其中，大桶和小桶的进价及售价如表所示．
大桶 | 小桶 | |
进价（元/个） | 18 | 5 |
售价（元/个） | 20 | 8 |
（1）该超市购进大桶和小桶各多少个？
（2）当小桶售出了300个后，商家决定将剩下的小桶的售价降低1元销售，并把其中一定数量的小桶作为赠品，在顾客购买大桶时，买一赠一（买一个大桶送一个小桶），送完即止．
请问：超市要使这批垃圾桶售完后获得的利润为1550元，那么小桶作为赠品送出多少个？
