Question

【题目】如图，在平面直角坐标系内，O为原点，点A的坐标为（﹣3，0），经过A、O两点作半径为的⊙C，交y轴的负半轴于点B．

（1）求B点的坐标；
（2）过B点作⊙C的切线交x轴于点D，求直线BD的解析式．

Answer 1

【答案】
（1）

解：∵∠AOB=90°，∴AB是直径，且AB=5，在Rt△AOB中，由勾股定理可得BO===4，∴B点的坐标为：（0，﹣4）

（2）

解：∵BD是⊙C的切线，CB是⊙C的半径，∴BD⊥AB，即∠ABD=90°，∴∠DAB+∠ADB=90°又∵∠BDO+∠OBD=90°，∴∠DAB=∠DBO，

∵∠AOB=∠BOD=90°，∴△ABO∽△BDO，∴，∴OD=，∴D的坐标为（，0）

设直线BD的解析式为y=kx+b（k≠0，k、b为常数），则有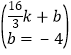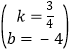，∴，∴直线BD的解析式为y=x﹣4．

【解析】由于∠AOB=90°，故AB是直径，且AB=5在Rt△AOB中，由勾股定理可得BO===4，则B点的坐标为（0，﹣4）；