题目内容
【题目】
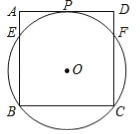
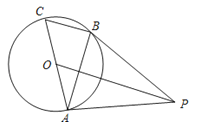
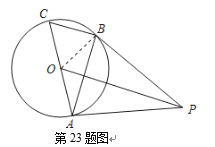
如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.
⑴求证:PB是⊙O的切线;
⑵连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
【答案】(1)详见解析;(2)2.
【解析】
试题分析:(1)连接OB,由AC是⊙O的直径可得∠ABC=90°,∠C+∠BAC=90°.再由OA=OB可得∠BAC=∠OBA. 又因∠PBA=∠C,所以∠PBA+∠OBA=90°,即PB⊥OB.即可判定PB是⊙O的切线.(2)可证△ABC∽△PBO,根据相似三角形的性质即可求BC的长.
试题解析: ⑴证明:如图所示,连接OB.
∵AC是⊙O的直径,
∴∠ABC=90°,∠C+∠BAC=90°.
∵OA=OB,
∴∠BAC=∠OBA.
∵∠PBA=∠C,
∴∠PBA+∠OBA=90°,即PB⊥OB.
∴PB是⊙O的切线.
⑵解:⊙O的半径为![]() ,∴OB=
,∴OB=![]() ,AC=
,AC=![]() .
.
∵OP∥BC,
∴∠BOP=∠OBC=∠C.
又∵∠ABC=∠PBO=90°,
∴△ABC∽△PBO,
∴![]() ,即
,即![]() .
.
∴BC=2.

【题目】观察表格,结合其内容中所蕴含的规律和相关知识可知b=__________;
列举 | 猜想与发现 |
3,4,5 | 32=4+5 |
5,12,13 | 52=12+13 |
7,24,25 | 72=24+25 |
… | … |
17,b,c | 172=b+c |
【题目】A.B两地果园分别有苹果20吨和30吨,C.D两地分别需要苹果15吨和35吨;已知从A.B到C.D的运价如下表:
到C地 | 到D地 | |
A果园 | 每吨15元 | 每吨12元 |
B果园 | 每吨10元 | 每吨9元 |
(1)若从A果园运到C地的苹果为x吨,则从A果园运到D地的苹果为 吨,从A果园将苹果运往D地的运输费用为 元。
(2)用含x的式子表示出总运输费。(结果要化简)
【题目】将一些数排列成下表:
第1列 | 第2列 | 第3列 | 第4列 | |
第1行 | 1 | 4 | 5 | 10 |
第2行 | 4 | 8 | 10 | 12 |
第3行 | 9 | 12 | 15 | 14 |
|
|
|
|
|
试探索:(请直接写出答案)
(1)第10行第2列的数是多少?
(2)数81所在的行和列分别是多少?
(3)数100所在的行和列分别是多少