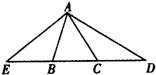
题目内容
如图(1)已知△ABC的外角∠CBD与∠BCE的平分线相交于点P,如图(2)已知△ABC的内角∠ABC与外角∠ACD的角平分线相交于点P.选择其中一个图形猜想∠BPC与∠A的关系并证明你的猜想
解:
我选择的是
证明:
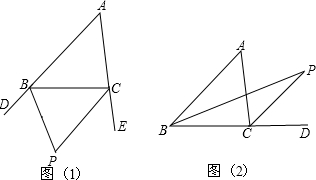
分析:图(1)中,根据三角形的内角和定理、角平分线定义和三角形的外角的性质进行推导,得∠BPC=90°-
∠A;
图(2)中,根据角平分线定义和三角形的外角的性质,可以得到∠BPC=
∠A.
| 1 |
| 2 |
图(2)中,根据角平分线定义和三角形的外角的性质,可以得到∠BPC=
| 1 |
| 2 |
解答: 解:图(1)
解:图(1)
∵∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,
∴∠DBC+∠ECB
=∠A+∠ACB+∠A+∠ABC
=180°+∠A,
∵BP,CP分别是△ABC外角∠DBC,∠BCE的角平分线,
∴∠PBC+∠PCB=
(∠DBC+∠ECB)=
(180+∠A)°,
即:∠BPC=180°-(∠PBC+∠PCB)=(90-
∠A)°;
图(2),结论:∠BPC=
∠A.
证明如下:
∵∠1是△PBC的外角,
∴∠P=∠1-∠2=
(∠ACD-∠ABC)=
∠A.
 解:图(1)
解:图(1)∵∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,
∴∠DBC+∠ECB
=∠A+∠ACB+∠A+∠ABC
=180°+∠A,
∵BP,CP分别是△ABC外角∠DBC,∠BCE的角平分线,
∴∠PBC+∠PCB=
| 1 |
| 2 |
| 1 |
| 2 |
即:∠BPC=180°-(∠PBC+∠PCB)=(90-
| 1 |
| 2 |
图(2),结论:∠BPC=
| 1 |
| 2 |
证明如下:
∵∠1是△PBC的外角,
∴∠P=∠1-∠2=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题要能够利用三角形的内角和定理及其推论、角平分线的定义推导角之间的关系.

练习册系列答案
相关题目
 20、如图所示,已知AB=AC,PB=PC,下面结论:(1)EB=EC;(2)AD⊥BC;(3)AE平分∠BEC;(4)∠PBC=∠PCB,其中正确的是( )
20、如图所示,已知AB=AC,PB=PC,下面结论:(1)EB=EC;(2)AD⊥BC;(3)AE平分∠BEC;(4)∠PBC=∠PCB,其中正确的是( )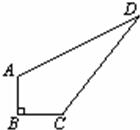 20、某住宅小区有一块草坪如图所示.已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,求这块草坪的面积.
20、某住宅小区有一块草坪如图所示.已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,求这块草坪的面积.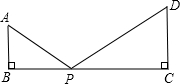 如图所示,已知AB⊥BC于B,CD⊥BC于C,AB=4,CD=6,BC=14,P为BC上一点,试问BP为何值时,△ABP与△PCD相似?
如图所示,已知AB⊥BC于B,CD⊥BC于C,AB=4,CD=6,BC=14,P为BC上一点,试问BP为何值时,△ABP与△PCD相似? 如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD,垂足为E.连接AC,OC,BC,若EB=8cm,CD=24cm,则⊙O的直径为
如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD,垂足为E.连接AC,OC,BC,若EB=8cm,CD=24cm,则⊙O的直径为