题目内容
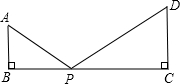如图所示，已知AB⊥BC于B，CD⊥BC于C，AB=4，CD=6，BC=14，P为BC上一点，试问BP为何值时，△ABP与△PCD相似？
分析：此题中P点的位置不同时，角的对应关系也不同，所以应分情况讨论：
（1）当∠A与∠DPC对应相等时；
（2）当∠A与∠D对应相等时；然后根据各自的对应线段成比例求出BP的长．
（1）当∠A与∠DPC对应相等时；
（2）当∠A与∠D对应相等时；然后根据各自的对应线段成比例求出BP的长．
解答：解：（1）当△ABP∽△PCD时，
=
，
=
，得BP=2或BP=12；
（2）当△ABP∽△DCP时，
=
，
=
，BP=5.6．
综合以上可知，当BP的值为2，12或5.6时，两三角形相似．
| AB |
| BP |
| PC |
| CD |
| 4 |
| BP |
| 14-BP |
| 6 |
（2）当△ABP∽△DCP时，
| AB |
| BP |
| CD |
| CP |
| 4 |
| BP |
| 6 |
| 14-BP |
综合以上可知，当BP的值为2，12或5.6时，两三角形相似．
点评：考查相似三角形的判定定理，注意对应角相等，对应边成比例．
练习册系列答案
相关题目
如图所示，已知AB∥EF∥CD，若AB=6厘米，CD=9厘米．求EF．
5、如图所示，已知AB∥CD，EF平分∠CEG，∠1=80°，则∠2的度数为（ ）
如图所示，已知AB为圆O的直径，AC为弦，OD∥BC交AC于D，OD=2cm，求BC的长．
如图所示，已知AB=AC，BD⊥AC，试说明∠BAC=2∠CBD．