题目内容
【题目】如图,已知,△ABC中,∠A=60,BD,CE是△ABC的两条角平分线,BD,CE相交于点O,求证:BC=CD+BE.

【答案】详见解析.
【解析】
在BC上找到F使得BF=BE,易证∠BOE=∠COD=60°,即可证明△BOE≌△BOF,可得∠BOF=∠BOE=60°,即可证明△OCF≌△OCD,可得CF=CD,根据BC=BF+CF即可解决问题.
证明:在BC上找到F使得BF=BE,
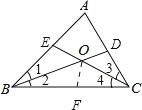
∵∠A=60°,BD、CE是△ABC的角平分线,
∴∠BOC=180°-![]() (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°-![]() (180°-∠A)=120°,
(180°-∠A)=120°,
∴∠BOE=∠COD=60°,
在△BOE和△BOF中,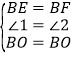 ,
,
∴△BOE≌△BOF,(SAS)
∴∠BOF=∠BOE=60°,
∴∠COF=∠BOC-∠BOF=60°,
在△OCF和△OCD中,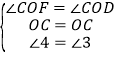 ,
,
∴△OCF≌△OCD(ASA),
∴CF=CD,
∵BC=BF+CF,
∴BC=BE+CD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






