题目内容
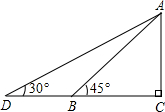
如图，湖中有建筑物AB，某人站在建筑物顶部A在岸上的投影处C，发现自己的影长与身高相等．他沿BC方向走30m到D处，测得顶部A的仰角为30°，求建筑物AB的高．
由C处人身高与影长相等可知，AB=CB．
设AB=xm，则BD=（x+30）m．
在Rt△ABD中，cotD=
，
∴ABcotD=BD．
xcot30°=x+30，
x=x+30，
（
-1）x=30，
∴x=
=15(
+1)=15
+15．
答：建筑物AB的高为（15
+15）m．
设AB=xm，则BD=（x+30）m．
在Rt△ABD中，cotD=
| BD |
| AB |
∴ABcotD=BD．
xcot30°=x+30，
| 3 |
（
| 3 |
∴x=
| 30 | ||
|
| 3 |
| 3 |
答：建筑物AB的高为（15
| 3 |
练习册系列答案
阅读快车系列答案
相关题目
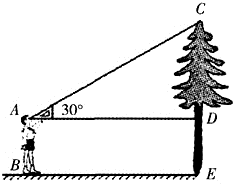
生进行测量树高的活动．通过分组活动，得到以下数据：
