题目内容
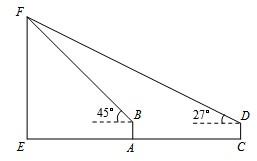
如图,某数学活动小组要测量旗杆的高度EF.小明与小亮在旗杆的同侧且相距10m的地方分别观测(点A、C、E在一直线上),小明的眼睛与地面的距离AB是1.6m,测得旗杆的顶部F的仰角是45°;小亮的眼睛与地面的距离CD是1.5m,测得旗杆的顶部F的仰角是27°.求旗杆的高度EF.(参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.50)

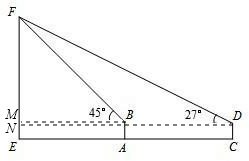
作BM⊥EF交EF于点M,DN⊥EF交EF于点N,
∵∠FBM=45°,
∴BM=FM,ME=AB=1.6,
设EF=x,则MB=x-1.6,
∴EC=x-1.6+10=x+8.4,
∵tan27°=
,
∴0.5=
,
解得x=11.4.
答:旗杆的高度EF高11.4m.
∵∠FBM=45°,
∴BM=FM,ME=AB=1.6,
设EF=x,则MB=x-1.6,
∴EC=x-1.6+10=x+8.4,
∵tan27°=
| FN |
| CE |
∴0.5=
| x-1.5 |
| x+8.4 |
解得x=11.4.
答:旗杆的高度EF高11.4m.


练习册系列答案
相关题目