题目内容
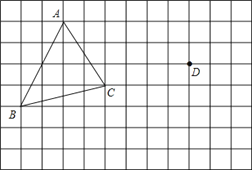
【题目】如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
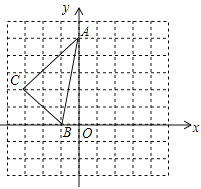
(1)画出将△ABC向右平移2个单位得到△A1B1C1;
(2)画出将△ABC绕点O顺时针方向旋转90°得到的△A2B2C2;
(3)求△A1B1C1与△A2B2C2重合部分的面积.
【答案】(1)作图见解析;(2)作图见解析;(3)![]() .
.
【解析】
试题分析:(1)将△ABC向右平移2个单位即可得到△A1B1C1.
(2)将△ABC绕点O顺时针方向旋转90°即可得到的△A2B2C2.
(3)B2C2与A1B1相交于点E,B2A2与A1B1相交于点F,如图,求出直线A1B1,B2C2,A2B2,列出方程组求出点E、F坐标即可解决问题.
试题解析:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
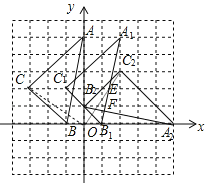
(3)B2C2与A1B1相交于点E,B2A2与A1B1相交于点F,如图,∵B2(0,1),C2(2,3),B1(1,0),A1(2,5),A2(5,0),∴直线A1B1为y=5x﹣5,直线B2C2为y=x+1,直线A2B2为![]() ,由
,由![]() 解得:
解得:![]() ,∴点E(
,∴点E(![]() ,
,![]() ),由
),由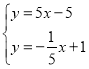 解得:
解得: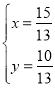 ,∴点F(
,∴点F(![]() ,
,![]() ),∴S△BEF=
),∴S△BEF=![]() =
=![]() ,∴△A1B1C1与△A2B2C2重合部分的面积为
,∴△A1B1C1与△A2B2C2重合部分的面积为![]() .
.

练习册系列答案
相关题目