Question

【题目】在一个不透明的盒子里装有若干个黑、白两种颜色球，这些球除颜色外其余完全相同．小颖做摸球实验，搅匀后，她从盒子里随机摸出一个球记下颜色后，再把球放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：

摸球的次数n	100	200	300	500	800	1000	3000
摸到白球的次数m	65	124	178	302	481	599	1803
摸到白球的频率	0.65	0.62	0.593	0.604	0.601	0.599	0.601

（1）若从盒子里随机摸出一个球，则摸到白球的概率估计值为　　　　 (精确到0.1)；

（2）若盒中黑球与白球若共有5个，小颖一次摸出两个球，请计算这两个球颜色不相同的概率，并说明理由．

Answer 1

【答案】（1）0.6；（2），理由见解析．

【解析】

（1）大量重复试验下摸球的频率可以估计摸球的概率，据此求解；

（2）画树状图列出所有等可能结果，再找到符合条件的结果数，根据概率公式求解可得．

解：（1）根据表中数据估计从盒中摸出一个球是白球的概率是0.6，

故答案为：0.6；

（2）由（1）可知，白球的个数为5×0.6=3，则黑球的个数为2，画树状图如下：

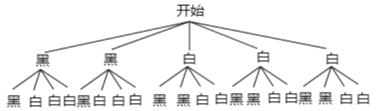
由表可知，所有等可能结果共有20种情况，

其中这两球颜色不同的有12种结果，

所以这两球颜色不同的概率为：．