题目内容
如图，在直角坐标系中，以原点为圆心，半径为5的圆内有一点P（0，-3），则经过点P的所有弦中最短的弦长为8
8
．分析：先画出最短弦，根据垂径定理求出AB=2PB=2AP，根据勾股定理求出BP，即可得出答案．
解答：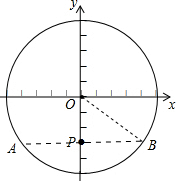
解：过P作弦AB⊥OP，则AB是过P点的⊙O的最短的弦，连接OB，
则由垂径定理得：AB=2AP=2BP，
在Rt△OPB中，PO=3，OB=5，由勾股定理得：PB=4，
则AB=2PB=8，
故答案为：8．
解：过P作弦AB⊥OP，则AB是过P点的⊙O的最短的弦，连接OB，则由垂径定理得：AB=2AP=2BP，
在Rt△OPB中，PO=3，OB=5，由勾股定理得：PB=4，
则AB=2PB=8，
故答案为：8．
点评：本题考查了垂径定理，勾股定理，坐标与图形性质等知识点，关键是找出符合条件的最短弦．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在直角坐标系中，点P的坐标为（3，4），将OP绕原点O逆时针旋转90°得到线段OP′．
，2）．画出△ABC的两个位似图形△A1B1C1，△A2B2C2，同时满足下列两个条件：