题目内容
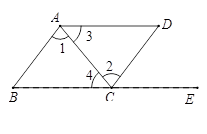
如图,AE平分∠BAD,DE平分∠ADC,AB⊥BC于B,∠1+∠2=90°,
说明:(1)AB∥CD;(2)DC⊥BC.
说明:(1)AB∥CD;(2)DC⊥BC.

(1)根据角平分线的性质可得∠BAE=∠1,∠CDE=∠2,再结合∠1+∠2=90°,即可得到∠BAD+∠CDA=180°,从而可以证得结论;
(2)根据垂直的性质可得∠ABC=90°,根据平行线的性质可得∠ABC+∠BCD=180°,即可得到∠BCD=90°,从而可以证得结论.
(2)根据垂直的性质可得∠ABC=90°,根据平行线的性质可得∠ABC+∠BCD=180°,即可得到∠BCD=90°,从而可以证得结论.
试题分析:(1)∵AE平分∠BAD,DE平分∠ADC,
∴∠BAE=∠1,∠CDE=∠2
∵∠1+∠2=90°
∴∠BAE+∠CDE=90°
∴∠BAD+∠CDA=180°
∴AB∥CD;
(2)∵AB⊥BC
∴∠ABC=90°
∵AB∥CD
∴∠ABC+∠BCD=180°
∴∠BCD=90°
∴DC⊥BC.
点评:解题的关键是熟练掌握角的平分线把角分成相等的两个小角,且都等于大角的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,∠E=20
,∠E=20




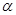 与∠
与∠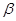 互余,且∠
互余,且∠