Question

如图，在三角形ABC中，点D、F在边BC上，点E在边AB上，点G在边AC上，AD∥EF，∠1+∠FEA＝180°．

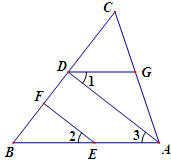
求证：∠CDG＝∠B．

Answer 1

∠CDG＝∠B．

试题分析：证明：∵AD∥EF，（已知）
∴∠2=∠3．（两直线平行，同位角相等） 2分
∵∠1+∠FEA=180°，∠2+∠FEA=180°， 3分
∴∠1=∠2．（同角的补角相等） 4分
∴∠1=∠3．（等量代换） 
∴DG∥AB．（内错角相等，两直线平行）……6分
∴∠CDG=∠B．（两直线平行，同位角相等）
点评：考查其性质及判定，熟练掌握，由题意可求之，本题属于基础题，难度不大。