题目内容
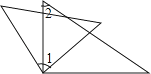
【题目】如图,已知点A、P在反比例函数y=![]() (k<0)的图象上,点B、Q在直线y=x﹣3的图象上,点B的纵坐标为﹣1,AB⊥x轴,且S△OAB=4,若P、Q两点关于y轴对称,设点P的坐标为(m,n).
(k<0)的图象上,点B、Q在直线y=x﹣3的图象上,点B的纵坐标为﹣1,AB⊥x轴,且S△OAB=4,若P、Q两点关于y轴对称,设点P的坐标为(m,n).
(1)求点A的坐标和k的值;
(2)求![]() 的值.
的值.
【答案】
(1)
解:∵点B在直线y=x﹣3的图象上,点B的纵坐标为﹣1,∴当y=﹣1时,x﹣3=﹣1,解得x=2,∴B(2,﹣1).
设点A的坐标为(2,t),则t<﹣1,AB=﹣1﹣t.∵S△OAB=4,∴![]() (﹣1﹣t)×2=4,解得t=﹣5,
(﹣1﹣t)×2=4,解得t=﹣5,
∴点A的坐标为(2,﹣5).∵点A在反比例函数y=![]() (k<0)的图象上,∴﹣5=
(k<0)的图象上,∴﹣5=![]() ,解得k=﹣10;
,解得k=﹣10;
(2)
解:∵P、Q两点关于y轴对称,点P的坐标为(m,n),∴Q(﹣m,n),∵点P在反比例函数y=﹣![]() 的图象上,点Q在直线y=x﹣3的图象上,
的图象上,点Q在直线y=x﹣3的图象上,
∴n=﹣![]() ,n=﹣m﹣3,∴mn=﹣10,m+n=﹣3,∴
,n=﹣m﹣3,∴mn=﹣10,m+n=﹣3,∴![]() .
.
【解析】(1)先由点B在直线y=x﹣3的图象上,点B的纵坐标为﹣1,将y=﹣1代入y=x﹣3,求出x=2,即B(2,﹣1).由AB⊥x轴可设点A的坐标为(2,t),利用S△OAB=4列出方程![]() (﹣1﹣t)×2=4,求出t=﹣5,得到点A的坐标为(2,﹣5);将点A的坐标代入y=
(﹣1﹣t)×2=4,求出t=﹣5,得到点A的坐标为(2,﹣5);将点A的坐标代入y=![]() ,即可求出k的值;
,即可求出k的值;
(2)根据关于y轴对称的点的坐标特征得到Q(﹣m,n),由点P(m,n)在反比例函数y=﹣![]() 的图象上,点Q在直线y=x﹣3的图象上,得出mn=﹣10,m+n=﹣3,再将
的图象上,点Q在直线y=x﹣3的图象上,得出mn=﹣10,m+n=﹣3,再将![]() 变形为
变形为![]() ,代入数据计算即可.
,代入数据计算即可.

练习册系列答案
相关题目