Question

【题目】如图，点A（1﹣，1+）在双曲线y=（x＜0）上．

（1）求k的值；
（2）在y轴上取点B（0，1），为双曲线上是否存在点D，使得以AB，AD为邻边的平行四边形ABCD的顶点C在x轴的负半轴上？若存在，求出点D的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：∵点A（1﹣，1+）在双曲线y=（x＜0）上，

∴k=（1﹣）（1+）=1﹣5=﹣4；

（2）

解：过点A作AE⊥y轴于点E，过点D作DF⊥x轴于点F，

∵四边形ABCD是以AB，AD为邻边的平行四边形ABCD，

∴DCAB，

∵A（1﹣，1+），B（0，1），

∴BE=，

由题意可得：DF=BE=，

则=，

解得：x=，

∴点D的坐标为：（﹣，）．

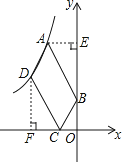
【解析】（1）直接利用反比例函数图象上点的坐标性质代入求出即可；
（2）根据平行四边形的性质得出D点纵坐标，进而代入函数解析式得出D点横坐标即可．
【考点精析】通过灵活运用平行四边形的性质，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分即可以解答此题．