Question

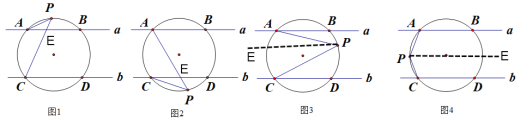
【题目】直线∥，一圆交直线a，b分别于A、B、C、D四点，点P是圆上的一个动点，连接PA、PC.

(1)如图1，直接写出∠PAB、∠PCD、∠P之间的数量关系为　 　 ；

(2)如图2，直接写出∠PAB、∠PCD、∠P之间的数量关系为　 　

(3)如图3，求证：∠P＝∠PAB+∠PCD；

(4)如图4，直接写出∠PAB、∠PCD、∠P之间的数量关系为 　 　.

Answer 1

【答案】（1）∠PCD＝∠P+∠PAB；（2）∠PAB＝∠P+∠PCD；（3）见解析；（4）∠PAB+∠P+∠PCD＝360°.

【解析】

(1)方法一：设AB、PC相交于点E，由外角性质得：∠PEB＝∠P+∠PAB，又因为a∥b，所以∠PEB＝∠PCD，从而求解；方法二：过点P作PE∥AB；

（2）方法一：设AP、CD相交于点E，理由同（1）得∠PED＝∠P+∠PCD，又因为a∥b，所以∠PED＝∠PAB，从而求解；方法二：过点P作PE∥AB；

(3) 过点P作PE∥a，因为a∥b，所以PE∥b，所以∠PAB=∠APE，∠∠PCD =∠EPC，

又因为∠APC=∠APE+∠CPE，所以∠APC＝∠PAB+∠PCD；

(4) ∠PAB+∠P+∠PCD＝360°. 过点P作PE∥a，因为a∥b，所以PE∥b，所以∠PAB+∠APE=180°，∠PCD+∠CPE=180°，即∠PAB+∠APE+∠PCD+∠CPE=360°，从而求解；

解 ：（1）∠PCD＝∠P+∠PAB；

理由：设AB、PC相交于点E，由外角性质得：∠PEB＝∠P+∠PAB，

∵a∥b，∴∠PEB＝∠PCD，

∴∠PCD＝∠P+∠PAB；

（2）∠PAB＝∠P+∠PCD；

理由：设AP、CD相交于点E，理由同（1）得∠PED＝∠P+∠PCD，

又∵a∥b，∴∠PED＝∠PAB，

∴ ∠PAB＝∠P+∠PCD ；

（3）过点P作PE∥a，∵a∥b，∴PE∥b，

∴∠PAB=∠APE，∠∠PCD =∠EPC，

∵∠APC=∠APE+∠CPE

∴∠APC＝∠PAB+∠PCD；；

(4) ∠PAB+∠P+∠PCD＝360°

理由：过点P作PE∥a，∵a∥b，∴PE∥b，

∴∠PAB+∠APE=180°，∠PCD+∠CPE=180°

∴∠PAB+∠APE+∠PCD+∠CPE=360°

即∠PAB+∠APC+∠PCD＝360°.