题目内容
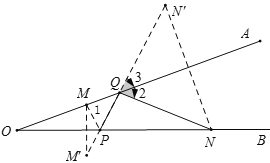
【题目】如图,∠AOB=20°,点M、N分别是边OA、OB上的定点,点P、Q分别是边OB、OA上的动点,记∠MPQ=![]() ,∠PQN=
,∠PQN=![]() ,当MP+PQ+QN最小时,则
,当MP+PQ+QN最小时,则![]() 的值为( )
的值为( )

A. 10°B. 20°C. 40°D. 60°
【答案】C
【解析】
作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,交OA于点Q,交OB于点P,则MP+PQ+QN最小,根据轴对称的性质以及平角的定义可得∠OPM=![]() (180°-α),再根据三角形外角的性质可得∠1=110°-
(180°-α),再根据三角形外角的性质可得∠1=110°-![]() α,同样根据平角的定义可得∠3=
α,同样根据平角的定义可得∠3=![]() (180°-β),由对顶角性质可得∠MQP=
(180°-β),由对顶角性质可得∠MQP=![]() (180°-β),根据三角形内角和定理可得∠1+∠MPQ+∠MQP=180°,即110°-
(180°-β),根据三角形内角和定理可得∠1+∠MPQ+∠MQP=180°,即110°-![]() α+α+
α+α+![]() (180°-β)=180°,整理即可求得答案.
(180°-β)=180°,整理即可求得答案.
如图,作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,交OA于点Q,交OB于点P,则MP+PQ+QN最小,
∵∠MPM′+∠MPQ=180°,∠OPM=∠OPM′,∠OPM+∠OPM′=∠MPM,∠MPQ=α,
∴∠OPM=![]() (180°-α),
(180°-α),
∵∠1=∠O+∠OPM,
∴∠1=20°+![]() (180°-α)=110°-
(180°-α)=110°-![]() α,
α,
∵∠2=∠3,∠2+∠3+∠MQN=180°,∠PQN=β,
∴∠3=![]() (180°-β),
(180°-β),
∴∠MQP=∠3=![]() (180°-β),
(180°-β),
在△PMQ中,∠1+∠MPQ+∠MQP=180°,
即110°-![]() α+α+
α+α+![]() (180°-β)=180°,
(180°-β)=180°,
∴β-α=40°,
故选C.

练习册系列答案
相关题目