题目内容
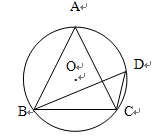
如图，⊙O是△ABC的外接圆，∠OCB=30°,则∠A的度数的等于( )
| A．30° | B．60° | C．15° | D．120° |
B
分析：在等腰三角形OCB中，求得两个底角∠OBC、∠0CB的度数，然后根据三角形的内角和求得∠COB=100°；最后由圆周角定理求得∠A的度数并作出选择．
解答：解：在△OCB中，OB=OC（⊙O的半径），
∴∠OBC=∠0CB（等边对等角）；
∵∠OCB=30°，∠C0B=180°-∠OBC-∠0CB，
∴∠COB=120°；
又∵∠A=
∠C0B（同弧所对的圆周角是所对的圆心角的一半），
∴∠A=60°，
故选B．
解答：解：在△OCB中，OB=OC（⊙O的半径），
∴∠OBC=∠0CB（等边对等角）；
∵∠OCB=30°，∠C0B=180°-∠OBC-∠0CB，
∴∠COB=120°；
又∵∠A=
∠C0B（同弧所对的圆周角是所对的圆心角的一半），∴∠A=60°，
故选B．
练习册系列答案
相关题目
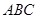与⊙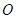
等高,如图放置, ⊙
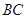相切于点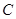
,⊙
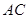相交于点
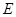,则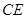
的长为 ㎝.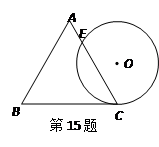
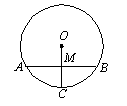
的两个根，且O1O2=7，则⊙O1、⊙O2的位置关系是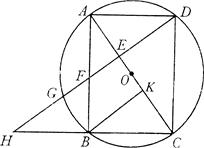
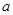，AD=
(
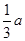，则a的值是( )
，
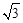