题目内容
【题目】(2014浙江金华)如图,矩形ABOD的两边OB,OD都在坐标轴的正半轴上,OD=3,另两边与反比例函数![]() (k≠0)的图象分别相交于点E、F,且DE=2.过点E作EH⊥x轴于点H,过点F作FG⊥EH于点G.回答下面的问题:
(k≠0)的图象分别相交于点E、F,且DE=2.过点E作EH⊥x轴于点H,过点F作FG⊥EH于点G.回答下面的问题:
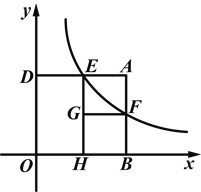
(1)①求反比例函数的解析式.
②当四边形AEGF为正方形时,求点F的坐标.
(2)小亮进一步研究四边形AEGF的特征后提出问题:“当AE>EG时,矩形AEGF与矩形DOHE能否全等?能否相似?”
针对小亮提出的问题,请你判断这两个矩形能否全等(直接写出结论即可).这两个矩形能否相似?若能相似,求出相似比;若不能相似,试说明理由.
【答案】(1)①![]() ②F(3,2) (2)不能全等
②F(3,2) (2)不能全等
【解析】(1)①∵四边形ABOD为矩形,EH⊥x轴,OD=3,DE=2,
∴E点坐标为(2,3).
∴k=2×3=6.
∴反比例函数解析式为![]() .
.
②设正方形AEGF的边长为a,则AE=AF=a,
∴A点坐标为(2+a,3),F点坐标为(2+a,3-a).
把点F的坐标代入![]() ,得(2+a)(3-a)=6,
,得(2+a)(3-a)=6,
解得a1=1,a2=0(舍去),
∴F点的坐标为(3,2).
(2)当AE>EG时,矩形AEGF与矩形DOHE不能全等.
理由如下:
假设矩形AEGF与矩形DOHE全等,则AE=OD=3,AF=DE=2,
∴A点坐标为(5,3),
∴F点坐标为(5,1),而5×1=5≠6,
∴F点不在反比例函数![]() 的图象上,
的图象上,
∴矩形AEGF与矩形DOHE不能全等.
当AE>EG时,矩形AEGF与矩形DOHE能相似.
由矩形AEGF与矩形DOHE相似,
得AE︰OD=AF︰DE,
∴![]() ,
,
设AE=3t,则AF=2t,
∴A点坐标为(2+3t,3),
∴F点坐标为(2+3t,3-2t),
把点F的坐标代入![]() ,得(2+3t)(3-2t)=6,
,得(2+3t)(3-2t)=6,
解得t1=0(舍去), ![]() ,
,
∴![]() ,
,
∴矩形AEGF与矩形DOHE的相似比为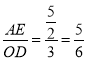 .
.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案