Question

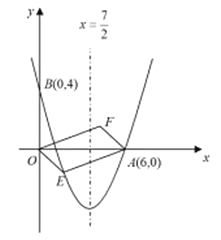
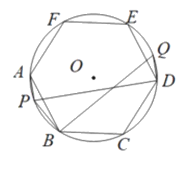
【题目】如图，正六边形ABCDEF内接于⊙O，在弧AB上取点P，连接AP，BP，过点D作DQ∥AP交⊙O于点Q，连接BQ． 已知BP=1，BQ=3，PQ的长为 ，AP的长为_____________．

Answer 1

【答案】，

【解析】

根据正六边形的性质过圆心O，则PQ也过圆心O，利用勾股定理可求得直径，在直角三角形PMB中，利用含30度角的直角三角形的性质求得BM、PM，再证得△ABM∽△QPB，可求得AM的长，即可求得结论．

连接PQ，，过B作AP的垂线交AP的延长线为M，

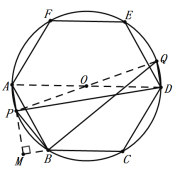
∵正六边形ABCDEF内接于⊙O，DQ∥AP，

∴过圆心O，

∴PQ也过圆心O，

∴∠PBQ=∠PDQ=90°，

∵BP=1，BQ=3，

∴PQ=；

即⊙O的直径为；

∴正六边形的边长AB=，

∵∠APB=∠APD+∠DPB =90°+60°=150°，

∴∠BPM=180°-∠APB =180°-150°=30°，

∴BM==，PM=BM=，

∵∠MAB=∠BQP，∠AMB=∠QBP=90°，

∴△ABM∽△QPB，

∴AM:MB=BQ:BP=3:1=3，

∴AM=，

∴AP=AM-PM=，

故答案为：，．