��Ŀ����
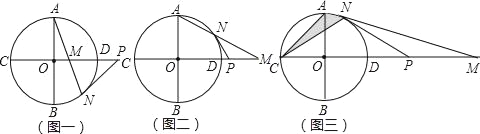
����Ŀ����ͼ����O�İ뾶Ϊ1��ֱ��CD����Բ��O������O��C��D���㣬ֱ��AB��CD����M��ֱ��CD�����ڵ�C��O��D��һ�����㣬AM���ڵ�ֱ�߽��ڡ�O�ڵ�N����P��ֱ��CD����һ�㣬��PM=PN��
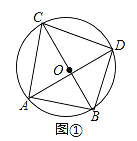
��1������M�ڡ�O�ڲ�����ͼһ�����ж�PN���O�Ĺ�ϵ����д��֤�����̣�
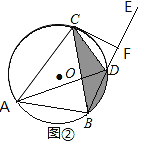
��2������M�ڡ�O�ⲿ����ͼ����������������ʱ����1���Ľ����Ƿ�������˵�����ɣ�
��3������M�ڡ�O�ⲿ����ͼ������AMO=15������ͼ����Ӱ���ֵ������
���𰸡���1��PN���O���У�֤������������2��������֤������������3��![]()
�������������������1���������ߵ��ж��ó���PNO=��PNM+��ONA=��AMO+��ONA����������ɣ�
��2��������֪�ó���PNM+��ONA=90���������ó���PNO=180��-90��=90�����ɵó��𰸣�
��3�����ȸ�����ǵ����ʵó���AON=60�������������������ʽ�ó����ɣ�
�����������1��PN����O����
֤��������ON��

����ONA=��OAN��
��PM=PN��
���PNM=��PMN��
�ߡ�AMO=��PMN��
���PNM=��AMO��
���PNO=��PNM+��ONA=��AMO+��ONA=90����
��PN����O����
��2��������
֤��������ON��

����ONA=��OAN��
��PM=PN��
���PNM=��PMN��
��Rt��AOM����OMA+��OAM=90����
���PNM+��ONA=90����
���PNO=180��-90��=90����
��PN����O����
��3������ON��

�ɣ�2����֪��ONP=90����
�ߡ�AMO=30����PM=PN��
���PNM=30������OPN=60����
���PON=30������AON=60����
��NE��OD��������E��
��NE=ONsin30��=1��![]() =
=![]() ��
��
S��Ӱ=S��AOC+S����AON-S��CON
=![]() OCOA+
OCOA+![]() ����12-
����12-![]() CONE
CONE
=![]() ��1��1+
��1��1+![]() ��-
��-![]() ��1��
��1��![]()
=![]() +
+![]() ����
����

 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�