题目内容
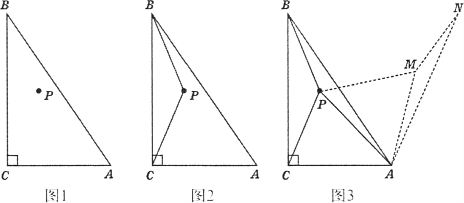
【题目】![]() 如图,点P是菱形ABCD的对角线BD上的一动点,连接CP并延长交AD于E,交BA的延长线于点F.
如图,点P是菱形ABCD的对角线BD上的一动点,连接CP并延长交AD于E,交BA的延长线于点F.
(1)求证:△APD≌△CPD.
(2)当菱形ABCD变为正方形,且PC=2,tan∠PFA= ![]() 时,求正方形ABCD的边长.
时,求正方形ABCD的边长.
【答案】
(1)解 :∵四边形ABCD是菱形 ,
∴DC=DA ,∠CDB=∠ADB
,又DP=DP ,
∴△APD≌△CPD.
(2)解 :∵△APD≌△CPD.
∴∠DAP=∠DCP,
∵CD∥BF,
∴∠DCP=∠F,
∴∠DAP=∠F,
又∵∠APE=∠FPA,
∴△APE∽△FPA,
∴AP∶FP=PE∶PA,
∴PA2=PEPF,
∵△APD≌△CPD,
∴PA=PC,
∴PC2=PEPF;
∵tan∠PFA= ![]() ,∠DCP=∠F,
,∠DCP=∠F,
∴tan∠DCP=![]() =
=![]() ,
,
∴DC=2DE ,
∵四边形ABCD是正方形 ,
∴DC=DA ,
∴DA=2DE ,
即点E是DA的中点 ,
∴DE=EA
在DCE与AFE中,
∵∠DCP=∠F
∠DEC=∠AEF
DE=AE
∴DCE≌AFE
∴EC=EF ,设PE=x ,则EC=EF=x+2 ,PF=2X+2
22=X·(2x+2)
解得 x1=-2 (舍去) ,x2=1 ,
∴CE=3 ,
再RtDEC中,设DE=y ,则DC=2y ,根据勾股定理得y2+(2y)2=32
解得 y±=![]() ,∴DE=
,∴DE=![]()
∴DC=![]() ,
,
即正方形的边长为![]()
【解析】(1)根据菱形的性质得出DC=DA ,∠CDB=∠ADB,又DP=DP ,从而利用AAS判断出△APD≌△CPD;
(2)首先由全等三角形的性质得出∠DAP=∠DCP,根据平行线的性质得出∠DCP=∠F,,从而得出∠DAP=∠F,又∠APE=∠FPA,故△APE∽△FPA ,根据相似三角行的性质得出AP∶FP=PE∶PA,即PA2=PEPF,又由全等三角形的性质得出PA=PC,从而得出PC2=PEPF;根据锐角三角函数的定义及等角的同名三角函数值相等得出DC=2DE ,根据正方形的性质得出DE=EA ,然后利用AAS判断出DCE≌AFE ,得出EC=EF ,设PE=x ,则EC=EF=x+2 ,PF=2X+2 ,从而得出关于x的方程求解得出x的值,从而得出CE的长,再RtDEC中,设DE=y ,则DC=2y ,根据勾股定理得出关于y的方程,求解得出y的值,进而得出正方形的边长。
【考点精析】掌握菱形的性质和正方形的性质是解答本题的根本,需要知道菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案