题目内容
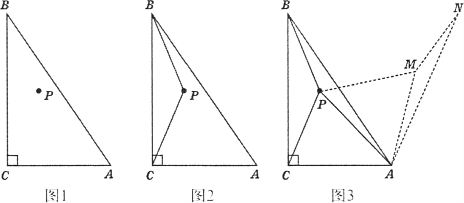
【题目】如图1,在△ABC中,∠ACB=90°,点P为ΔABC内一点.
(1)连接PB,PC,将ABCP沿射线CA方向平移,得到ΔDAE,点B,C,P的对应点分别为点D、A、E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,BP=3,AB=6,求CE的长
(2)如图3,以点A为旋转中心,将ΔABP顺时针旋转60°得到△AMN,连接PA、PB、PC,当AC=3,AB=6时,根据此图求PA+PB+PC的最小值.
【答案】(1)①补图见解析;②![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据作平移图形的方法作图即可;(2)证明四边形BCAD是矩形,得到CD=AB=6,由平移的性质得DE=BP=3,由BP⊥CE,BP∥DE得到△DEC是直角三角形,根据![]() 即可求出CE的长度;(3)当C、P、M、N四点共线时,PA+PB+PC最小,由旋转可得,△AMN≌△APB, PB=MN,易得△APM、△ABN都是等边三角形,所以PA=PM,则PA+PB+PC=PM+MN+PC=CN,所以BN=AB=6,∠BNA=60°,∠PAM=60°,根据∠CAN=∠CAB+∠BAN=120°,所以∠CBN=90°,在Rt△ABC中,求得
即可求出CE的长度;(3)当C、P、M、N四点共线时,PA+PB+PC最小,由旋转可得,△AMN≌△APB, PB=MN,易得△APM、△ABN都是等边三角形,所以PA=PM,则PA+PB+PC=PM+MN+PC=CN,所以BN=AB=6,∠BNA=60°,∠PAM=60°,根据∠CAN=∠CAB+∠BAN=120°,所以∠CBN=90°,在Rt△ABC中,求得![]() ,在Rt△BCN中,
,在Rt△BCN中, ![]() 即为所求;
即为所求;
试题解析:
解:(1)①补全图形如图所示;
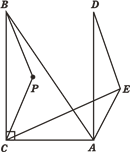
②如图,连接BD、CD,如图所示:
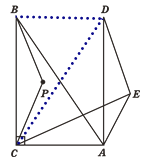
∵△BCP沿射线CA方向平移,得到△DAE,
∴BC∥AD且BC=AD,
∵∠ACB=90°,
∴四边形BCAD是矩形,
∴CD=AB=6,
∵BP=3,
∴DE=BP=3,
∵BP⊥CE,BP∥DE,
∴DE⊥CE,
∴在Rt△DCE中, ![]() ;
;
(2)证明:如图,当C、P、M、N四点共线时,PA+PB+PC最小
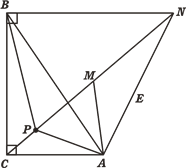
由旋转可得,△AMN≌△APB,
∴PB=MN
易得△APM、△ABN都是等边三角形,
∴PA=PM
∴PA+PB+PC=PM+MN+PC=CN,
∴BN=AB=6,∠BNA=60°,∠PAM=60°
∴∠CAN=∠CAB+∠BAN=60°+60°=120°,
∴∠CBN=90°
在Rt△ABC中,易得![]()
∴在Rt△BCN中, ![]()

【题目】NBA季后赛正如火如荼地进行着,詹姆斯率领的骑士队在第三场季后赛中先落后25分的情况下实现了大逆转.该场比赛中詹姆斯的技术统计数据如下表所示:
技术 | 上场时间 | 投篮次数 | 投中次数 | 罚球得分 | 篮板个数 | 助攻次数 | 个人总得分 |
数据 | 45 | 27 | 14 | 7 | 13 | 12 | 41 |
(表中投篮次数和投中次数均不包括罚球,个人总得分来自2分球和3分球的得分以及罚球得分)根据以上信息,求出本场比赛中詹姆斯投中2分球和3分球的个数.
