题目内容
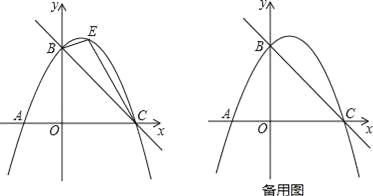
【题目】(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABE和等边△ACD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分别以AB、AC为边向外作正方形ABNE和正方形ACMD,连接BD,求BD的长.
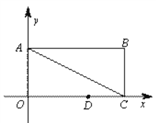
(3)如图3,在(2)的条件下,以AC为直角边在线段AC的左侧作等腰直角△ACD,求BD的长.

【答案】(1)BD =CE,理由见解析;(2)BD长是![]() cm; (3) BD长是(
cm; (3) BD长是(![]() -3)cm.
-3)cm.
【解析】试题分析:(1)证明△EAC与△BAD全等即可得证;
(2)连接EC、EB,通过证明△EAC与△BAD 全等,得到BD=CE.由勾股定理可得EC的长,从而可得BD长;
(3)如图,在线段AC的右侧过点A作AE⊥AB于A,交BC的延长线于点E,通过证明△EAC与△BAD全等,从而得BD=CE,从而求得BD长.
试题解析:(1)BD =CE.
理由:∵△ABE和△ACD都是等边三角形,∴∠BAE=∠CAD=60°,AE=AB,AC=AD,
∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD, ∴△EAC≌△BAD (SAS) ,∴BD=CE.
(2)如图,连接EC、EB.
在正方形ABNE和正方形ACMD中
∵![]() ,AE=AB ,∠BAE=
,AE=AB ,∠BAE=![]() ,∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,∴△EAC≌△BAD (SAS) ,∴BD=CE.
,∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,∴△EAC≌△BAD (SAS) ,∴BD=CE.
∵AE=AB=5,∴BE=![]() , ∠ABE=∠AEB=45.
, ∠ABE=∠AEB=45.
又∵∠ABC=45,∴∠ABC+∠ABE=45+45=90, ∴EC=![]() =
=![]() =
=![]() ,
,
∴BD=CE=![]() (cm).
(cm).
答:BD长是![]() cm.
cm.

(3)如图,在线段AC的右侧过点A作AE⊥AB于A,交BC的延长线于点E,
∴∠BAE=90,
又∵∠ABC=45,∴∠E=∠ABC=45,∴AE=AB=5,BE=![]() =
=![]() .
.
又∵∠ACD=∠ADC=45 ,∴∠BAE= ∠DAC=90, ∴∠BAE![]() ∠BAC=∠DAC
∠BAC=∠DAC![]() ∠BAC,
∠BAC,
即∠EAC=∠BAD,∴△EAC≌△BAD (SAS) , ∴BD=CE.
∵BC=3,∴BD=CE=(![]() -3)(cm).
-3)(cm).
答:BD长是(![]() -3)cm.
-3)cm.


 阅读快车系列答案
阅读快车系列答案