ЬтФПФкШн
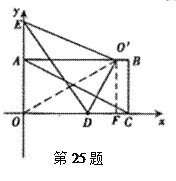
ЁОЬтФПЁПШчЭМ,дкЦНУцжБНЧзјБъЯЕжа,ОиаЮOABCЕФБпOAдкyжсЕФе§АыжсЩЯ,OCдкxжсЕФе§АыжсЩЯЃЌOA=1,OC=2,ЕуDдкБпOCЩЯЧвOD=1.25ЃЎ
ЃЈ1ЃЉЧѓжБЯпACЕФНтЮіЪНЃЎ
ЃЈ2ЃЉдкyжсЩЯЪЧЗёДцдкЕуP,жБЯпPDгыОиаЮЖдНЧЯпACНЛгкЕуM,ЪЙЕУЁїDMCЮЊЕШбќШ§НЧаЮЃПШєДцдк,жБНгаДГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉХзЮяЯпy=-x2ОЙ§дѕбљЦНвЦ,ВХФмЪЙЕУЦНвЦКѓЕФХзЮяЯпЙ§ЕуDКЭЕуEЃЈЕуEдкyжсе§АыжсЩЯЃЉ,ЧвЁїODEбиDEелЕўКѓЕуOТфдкБпABЩЯO/ДІЃП
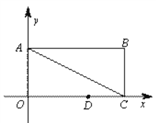
ЁОД№АИЁПНтЃКЃЈ1ЃЉOA=1ЃЌOC=2
дђAЕузјБъЮЊЃЈ0ЃЌ1ЃЉЃЌCЕузјБъЮЊЃЈ2ЃЌ0ЃЉ
ЩшжБЯпACЕФНтЮіЪНЮЊy=kx+b
![]()
НтЕУ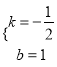
![]() жБЯпACЕФНтЮіЪНЮЊ
жБЯпACЕФНтЮіЪНЮЊ![]()
ЃЈ2ЃЉ![]() Лђ
Лђ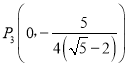
ЃЈ3ЃЉШчЭМЃЌЩш![]()
Й§![]() Еузї
Еузї![]() гкF
гкF
![]()
гЩелЕўжЊ![]()
![]()
![]() Лђ2
Лђ2
ЁОНтЮіЁПТд

СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП