题目内容
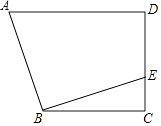
【题目】如图，三角形纸片中，AB=8cm，BC=6cm，AC=5cm．沿过点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD，求△ADE的周长． 
【答案】解：∵BC沿BD折叠点C落在AB边上的点E处，
∴DE=CD，BE=BC，
∵AB=8cm，BC=6cm，
∴AE=AB﹣BE=AB﹣BC=8﹣6=2cm，
∴△ADE的周长=AD+DE+AE，
=AD+CD+AE，
=AC+AE，
=5+2，
=7cm．
【解析】根据翻折变换的性质可得DE=CD，BE=BC，然后求出AE，再根据三角形的周长列式求解即可．
【考点精析】根据题目的已知条件，利用翻折变换（折叠问题）的相关知识可以得到问题的答案，需要掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
【题目】为了深化课程改革，省实验积极开展校本课程建设，计划成立“增量阅读”、“趣味数学”、“音乐舞蹈”和“戏剧英语”等多个社团，要求每位学生都自主选择其中一个社团，为此，随机调查了初中部分学生选择社团的意向．并将调查结果绘制成如下统计图表（不完整）：
选择意向 | 增量阅读 | 趣味数学 | 音乐舞蹈 | 戏曲英语 | 其他 |
所占百分比 | a | 20% | b | 10% | 5% |
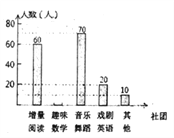
根据统计图表的信息，解答下列问题：
(l)求本次抽样调查的学生总人数及a、b的值：
(2)将条形统计图补充完整；
(3)若该校共有5000名学生，试估计全校选择“音乐舞蹈”社团的学生人数．
