题目内容
【题目】已知:关于x的一元二次方程mx2-3(m-1)x+2m-3=0(m>3).
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两个实数根分别为x1,x2,且x1<x2.
①求方程的两个实数根x1,x2(用含m的代数式表示);
②若mx1<8-4x2,直接写出m的取值范围.
【答案】(1)证明见解析;(2)①x1=1,x2=![]() ;②
;②![]() .
.
【解析】(1)由于m>3,此方程为关于x的一元二次方程,再计算出判别式△=(m-3)2,然后根据判别式的意义即可得到结论;
(2)②由求根公式得到x=1,或x=![]() ,即可得到结论;②根据mx1<8-4x2,即可得到 结果.
,即可得到结论;②根据mx1<8-4x2,即可得到 结果.
(1)证明:∵mx2-3(m-1)x+2m-3=0(m>3)是关于x的一元二次方程,
∴△=[(-3(m-1)]2-4m(2m-3)=m2-6m+9=(m-3)2,
∵m>3,
∴(m-3)2>0,即△>0,
∴方程总有两个不相等的实数根;
(2)①由求根公式得x=![]() ,
,
∴x=1,或x=![]() ,
,
当x1=1,x2=2-![]() ,
,
②则mx1<8-4x2,
即m<8-8+![]() ,
,
∴3<m<2![]() ;
;
当x1=2-![]() ,x2=1,
,x2=1,
则2m-3<4,
∴3<m<![]() .
.
综上所述,3<m<2![]() .
.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
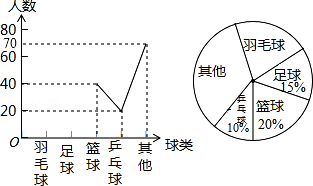
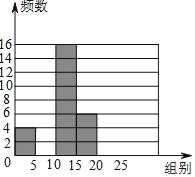
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】珠海市某中学开展主题为“我爱阅读”的专题调查活动,为了解学校1200名学生一年内阅读书籍量,随机抽取部分学生进行统计,绘制成如下尚未完成的频数分布表和频数分布直方图.请根据图表,解答下面的问题:
分组 | 频数 | 频率 |
0≤x<5 | 4 | 0.08 |
5≤x<10 | 14 | 0.28 |
10≤x<15 | 16 | a |
15≤x<20 | b | c |
20≤x<25 | 10 | 0.2 |
合计 | d | 1.00 |
(1)a= ,b= c= .
(2)补全频数分布直方图;
(3)根据该样本,估计该校学生阅读书籍数量在15本或15本以上的人数.
【题目】父亲告诉小明:“距离地面越高,温度越低”,并给小明出示了下面的表格:
距离地面高度(千米)h | 0 | 1 | 2 | 3 | 4 | 5 |
温度(℃)t | 20 | 14 | 8 | 2 | ﹣4 | ﹣10 |
根据表中,父亲还给小明出了下面几个问题,请你帮助小明回答下列问题:
(1)表中自变量是 ;因变量是 ;当地面上(即h=0时)时,温度是 ℃.
(2)如果用h表示距离地面的高度,用t表示温度,请写出满足t与h关系的式子.
(3)计算出距离地面6千米的高空温度是多少?