题目内容
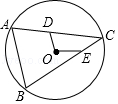
【题目】∠AOB与∠COD有共同的顶点O,其中∠AOB=∠COD=60°.
(1)如图①,试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)如图①,若∠BOC=10°,求∠AOD的度数;
(3)如图①,猜想∠AOD与∠BOC的数量关系,并说明理由;
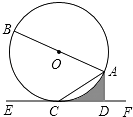
(4)若改变∠AOB,∠COD的位置,如图②,则(3)的结论还成立吗?若成立,请证明;若不成立,请直接写出你的猜想.

【答案】(1)∠AOC=∠BOD;(2)110°;(3)∠AOD+∠COB=120°;(4)不成立,猜想:∠AOD+∠BOC=240°.
【解析】
(1)利用角的和差定义证明即可;
(2)求出∠AOC即可解决问题;
(3)结论:∠AOD+∠COB=120°.利用角的和差定义证明即可;
(4)不成立.猜想:∠AOD+∠BOC=240°,根据周角的性质证明即可;
(1)结论:∠AOC=∠BOD.理由如下:
∵∠AOB=∠COD=60°,∴∠AOC+∠BOC=∠BOD+∠BOC,∴∠AOC=∠BOD.
(2)∵∠BCO=10°,∠AOB=60°,∴∠AOC=50°,∴∠AOD=∠AOC+∠COD=50°+60°=110°.
(3)猜想:∠AOD+∠COB=120°.理由如下:
∵∠AOB=∠COD=60°,∴∠AOD=∠AOB+∠COD﹣∠COB=120°﹣∠COB,∴∠AOD+∠COB=120°.
(4)不成立.猜想:∠AOD+∠BOC=240°.理由如下:
∵∠AOB=∠COD=60°,∴∠AOD+∠BOC=360°﹣60°﹣60°=240°.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目