题目内容
【题目】问题情境:
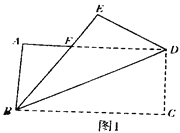
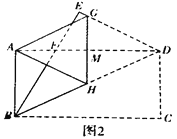
在综合实践课上,张老师让同学们以“矩形的折叠”为主题开展数学活动,张老师拿着一张矩形纸片ABCD,其中AB=acm, AD=bcm, 如图1,先沿对角线BD折叠,点C落在点E的位置,BE交AD于点F.
操作发现:
(1)“奋进”小组发现与BF的长度一定相等的线段是哪一条;
(2)如图2.“雄鹰”小组将图1再折叠一次,使点D与点A重合,得到折痕GH,GH交AD于点M,发现△DGH是等腰三角形,请你证明这个结论;
实践探究:
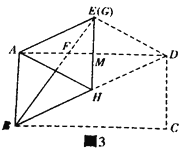
(3)“创新”小组将自己准备的矩形纸片按照(2)中“雄鹰”小组的作法操作,发现点E和点G重合,,如图3,试探究“创新”小组准备的矩形纸片中a与b满足的数量关系;
(4)”爱心”小组在其他小组的基础上提出问题:当a与b满足什么关系时,点G是DE的中点?请你直接出a与b满足的关系.
【答案】(1)BF=DF,(2)△DGH是等腰三角形,(3)b=![]() (4)a=b
(4)a=b
【解析】
(1)根据折叠的条件,证明△AFB≌△EFD(AAS)即可解题,
(2)找到对称轴,证明GH平行CD,利用内错角相等得∠GHD=∠HDC,由折叠得∠GDH=∠GHD,等量代换得∠GDH=∠GHD,等角对等边即可解题.
(3)在Rt△BED中利用斜边中线等于斜边一半,得BD=2EH,根据已知,用代数式表示出BD和EH的长即可解题,
(4)根据题意,证明四边形ABCD是正方形,即可直接写出a=b的结论.
解:(1)BF=DF,
由折叠可知:AB=DE,∠A=∠E,∠AFB=∠EFD,
∴△AFB≌△EFD(AAS)
∴BF=DF,
(2)由(1)可知∠GDH=∠HDC
由图可知:GH为对称轴,点D和点A关于GH对称,即GH垂直平分AD,
∵四边形ABCD是矩形,AD⊥CD,
∴GH∥CD,
∴∠GHD=∠HDC
∴∠GDH=∠GHD
∴△DGH是等腰三角形,
(3)由题可知,点H为对角线BD上的中点,EH=ED,
在Rt△BED中,BD=2EH(斜边中线等于斜边一半)
∵AB=acm, AD=bcm,
∴EH=ED=AB= a,BD=![]()
∴![]() =a,整理得:b=
=a,整理得:b=![]()
(4)a=b
理由:根据题意可知,GH为中位线,GH∥EB,点A与E重合,此时图形为正方形,
故a=b

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案