题目内容
如图,直线y=kx+4与函数y=| m |
| x |
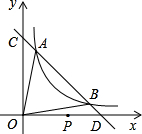 D两点.
D两点.(1)若△COD的面积是△AOB的面积的
| 2 |
(2)在(1)的条件下,是否存在k和m,使得以AB为直径的圆经过点P(2,0)?若存在,求出k和m的值;若不存在,请说明理由.
分析:(1)根据直线的解析式求得点C,D的坐标,从而表示出△COD的面积;根据两个函数的解析式联立解方程组求得点A,B的坐标,从而根据△AOD的面积减去△BOD的面积表示出△AOB的面积,再根据两个三角形之间的面积关系表示出k与m之间的函数关系式;
(2)假设存在,根据直径所对的圆周角是直角,得到AP⊥BP,从而得到Rt△MAP∽Rt△NPB.再根据相似三角形的对应边的比相等,得到关于k,m的关系式,结合(1)中的结论进行求解.
(2)假设存在,根据直径所对的圆周角是直角,得到AP⊥BP,从而得到Rt△MAP∽Rt△NPB.再根据相似三角形的对应边的比相等,得到关于k,m的关系式,结合(1)中的结论进行求解.
解答:解:(1)设A(x1,y1),B(x2,y2)(其中x1<x2,y1>y2),
∵S△COD=
S△AOB,
∴S△COD=
(S△AOD-S△BOD)
∴
•OC•OD=
(
•OD•y1-
•OD•y2),OC=
(y1-y2),(2分)
又OC=4,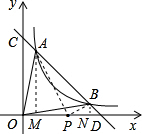
∴(y1-y2)2=8,即(y1+y2)2-4y1y2=8,(3分)
由y=
可得x=
,代入y=kx+4可得:y2-4y-km=0①
∴y1+y2=4,y1•y2=-km,
∴16+4km=8,即k=-
又方程①的判别式△=16+4km=8>0,
∴所求的函数关系式为k=-
(m>0);(5分)
(2)假设存在k,m,使得以AB为直径的圆经过点P(2,0)
则AP⊥BP,过A、B分别作x轴的垂线,垂足分别为M、N
∵∠MAP与∠BPN都与∠APM互余,
∴∠MAP=∠BPN(6分)
∴Rt△MAP∽Rt△NPB,
∴
=
∴
=
,
∴(x1-2)(x2-2)+y1y2=0,
∴(
-2)(
-2)+y1y2=0,
即m2-2m(y1+y2)+4y1y2+(y1y2)2=0②(8分)
由(1)知:y1+y2=4,y1•y2=2,代入②得:m2-8m+12=0,
∴m=2或6,又k=-
,
∴
或
,
∴存在k,m,使得以AB为直径的圆经过点P(2,0),且
或
.(10分)
∵S△COD=
| 2 |
∴S△COD=
| 2 |
∴
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
又OC=4,

∴(y1-y2)2=8,即(y1+y2)2-4y1y2=8,(3分)
由y=
| m |
| x |
| m |
| y |
∴y1+y2=4,y1•y2=-km,
∴16+4km=8,即k=-
| 2 |
| m |
又方程①的判别式△=16+4km=8>0,
∴所求的函数关系式为k=-
| 2 |
| m |
(2)假设存在k,m,使得以AB为直径的圆经过点P(2,0)
则AP⊥BP,过A、B分别作x轴的垂线,垂足分别为M、N
∵∠MAP与∠BPN都与∠APM互余,
∴∠MAP=∠BPN(6分)
∴Rt△MAP∽Rt△NPB,
∴
| AM |
| PN |
| MP |
| NB |
∴
| y1 |
| x2-2 |
| 2-x1 |
| y2 |
∴(x1-2)(x2-2)+y1y2=0,
∴(
| m |
| y1 |
| m |
| y2 |
即m2-2m(y1+y2)+4y1y2+(y1y2)2=0②(8分)
由(1)知:y1+y2=4,y1•y2=2,代入②得:m2-8m+12=0,
∴m=2或6,又k=-
| 2 |
| m |
∴
|
|
∴存在k,m,使得以AB为直径的圆经过点P(2,0),且
|
|
点评:能够根据直线的解析式求得与坐标轴的交点的坐标;能够把不规则三角形的面积进行转换.

练习册系列答案
相关题目
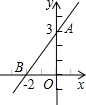 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
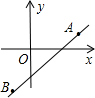 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
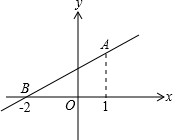 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为