题目内容
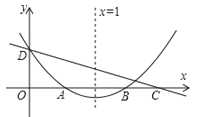
【题目】如图,在平面直角坐标系中,将一块腰长为![]() 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(![]() ,0),点B在抛物线
,0),点B在抛物线![]() 上.
上.
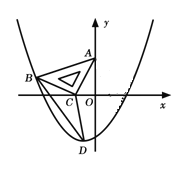
(1)点A的坐标为 ,点B的坐标为 ;
(2)抛物线的解析式为 ;
(3)设(2)中抛物线的顶点为D,求△DBC的面积;
(4)在抛物线上是否还存在点P(点B除外),使ΔACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由。
【答案】(1)A(0,2),B(![]() ,1).
,1).
(2)![]() .
.
(3)15/8
(4)存在,
点P的坐标为(1,-1)和(2,1)
【解析】(1)A(0,2),B(![]() ,1).
,1).
(2)![]() .
.
(3)如图1,可求得抛物线的顶点D(![]() ).
).
设直线BD的关系式为![]() , 将点B、D的坐标代入,求得
, 将点B、D的坐标代入,求得![]() ,
, ![]() ,
,
∴BD的关系式为![]() .
.
设直线BD和x轴交点为E,则点E(![]() ,0),CE=
,0),CE=![]() .
.
∴ △DBC的面积为![]() .
.
(4)存在,
点P的坐标为(1,-1)和(2,1)
(1)根据腰长为![]() 的等腰Rt△ABC(∠C=90°),由AC=
的等腰Rt△ABC(∠C=90°),由AC=![]() ,CO=1,求出AO即可得出A点的坐标,进而得出B点的坐标;
,CO=1,求出AO即可得出A点的坐标,进而得出B点的坐标;
(2)将B点坐标代入y=ax2+ax-2即可得出二次函数解析式;
(3)由(2)得顶点D的坐标,从而求得BD的关系式,设直线BD和x轴交点为E,可求得E点坐标,求得CE长,最后求得△DBC的面积
(4)延长BC到P,使CP=BC,连接AP,利用等腰直角三角形的性质与全等三角形的判定与性质解答即可.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目