题目内容
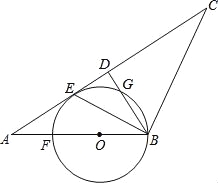
【题目】如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于点F,交BC于点E,过点E作EG⊥AB于G,连结GF.求证:四边形CFGE是菱形.
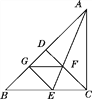
【答案】见解析
【解析】试题分析:本题,角的平分线,可以得到△AEG![]() △AEC,GE=EC,△AFG
△AEC,GE=EC,△AFG![]() △AFC,GF=FC, EC⊥AC,EG⊥AB,FC=EC,可以证明四边形CFGE是菱形.
△AFC,GF=FC, EC⊥AC,EG⊥AB,FC=EC,可以证明四边形CFGE是菱形.
试题解析:
由∠ACB=90°,AE平分∠BAC,EG⊥AB,
易证△ACE≌△AGE,
∴CE=EG,∠AEC=∠AEG.
∵CD是AB边上的高,EG⊥AB,
∴EG∥CD,
∴∠EFC=∠AEG,
∴∠EFC=∠AEC,
∴FC=EC,∴FC=EG,
∴四边形CFGE是平行四边形.
又∵GE=CE,
∴四边形CFGE是菱形.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目