题目内容
【题目】学生在操场上利用三角函数测量旗杆AB的高,直线l为水平地面,两个同学把30°的三角板和量角器按如图所示的方式垂直放在地面上,量角器的零刻度线与地面重合,此时旗杆顶部B的影子恰好落在三角形板的顶点D处和量角器37°的刻度C处,已知三角形板的边DE=60厘米,量角器的半径r=25厘米,量角器的圆心O到A的距离为5米. 
(1)则∠AOC=°(直接写出答案)
(2)求旗杆AB的高度(精确到0.1米,参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75, ![]() ≈1.73)
≈1.73)
【答案】
(1)37
(2)解:过C作CP⊥直线l,过C作CM⊥AB于M,过D作N⊥AB于N,
在Rt△OCP中,CP=OCsin37°≈0.25×0.6=0.15米,OP=OCcos37°≈0.25×0.8=0.2米;
∵CM⊥AB,DN⊥AB,
∴CM∥DN,
∴△BND∽△BMC,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AB≈5.6米,
答:旗杆AB的高度为5.6米.
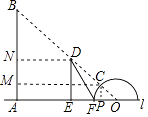
【解析】解:(1)∠AOC=37°,
所以答案是:37;

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目