题目内容
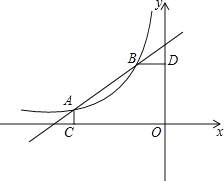
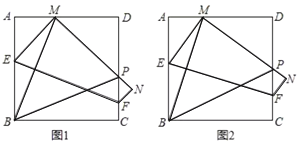
【题目】如图1.在边长为10的正方形![]() 中,点
中,点![]() 在边
在边![]() 上移动(点
上移动(点![]() 不与点
不与点![]() ,
,![]() 重合),
重合),![]() 的垂直平分线分别交
的垂直平分线分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,将正方形
,将正方形![]() 沿
沿![]() 所在直线折叠,则点
所在直线折叠,则点![]() 的对应点为点
的对应点为点![]() ,点
,点![]() 落在点
落在点![]() 处,
处,![]() 与
与![]() 交于点
交于点![]() ,
,
(1)若![]() ,求
,求![]() 的长;
的长;
(2)随着点![]() 在边
在边![]() 上位置的变化,
上位置的变化,![]() 的度数是否发生变化?若变化,请说明理由;若不变,请求出
的度数是否发生变化?若变化,请说明理由;若不变,请求出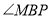 的度数;
的度数;
(3)随着点![]() 在边
在边![]() 上位置的变化,点
上位置的变化,点![]() 在边
在边![]() 上位置也发生变化,若点
上位置也发生变化,若点![]() 恰好为
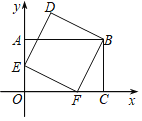
恰好为![]() 的中点(如图2),求
的中点(如图2),求![]() 的长.
的长.
【答案】(1)![]() ;(2)不变,45°;(3)
;(2)不变,45°;(3)![]() .
.
【解析】
(1)由翻折可知:EB=EM,设EB=EM=x,在Rt△AEM中,根据EM2=AM2+AE2,构建方程即可解决问题.
(2)如图1-1中,作BH⊥MN于H.利用全等三角形的性质证明∠ABM=∠MBH,∠CBP=∠HBP,即可解决问题.
(3)如图2中,作FG⊥AB于G.则四边形BCFG是矩形,FG=BC,CF=BG.设AM=x,在Rt△DPM中,利用勾股定理构建方程求出x,再在Rt△AEM中,利用勾股定理求出BE,EM,AE,再证明AM=EG即可解决问题.
(1)如图1中,
∵四边形ABCD是正方形,
∴∠A=90°,AB=AD=10,
由翻折可知:EB=EM,设EB=EM=x,
在Rt△AEM中,∵EM2=AM2+AE2,
∴x2=42+(10-x)2,
∴x=![]() .
.
∴BE=![]() .
.
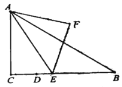
(2)如图1-1中,作BH⊥MN于H.
∵EB=EM,
∴∠EBM=∠EMB,
∵∠EMN=∠EBC=90°,
∴∠NMB=∠MBC,
∵AD∥BC,
∴∠AMB=∠MBC,
∴∠AMB=∠BMN,
∵BA⊥MA,BH⊥MN,
∴BA=BH,
∵∠A=∠BHM=90°,BM=BM,BA=BH,
∴Rt△BAM≌△BHM(HL),
∴∠ABM=∠MBH,
同法可证:∠CBP=∠HBP,
∵∠ABC=90°,
∴∠MBP=∠MBH+∠PBH=![]() ∠ABH+
∠ABH+![]() ∠CBH=
∠CBH=![]() ∠ABC=45°.
∠ABC=45°.
∴∠PBM=45°.
(3)如图2中,作FG⊥AB于G.则四边形BCFG是矩形,FG=BC,CF=BG.设AM=x,
∵PC=PD=5,
∴PM+x=5,DM=10-x,
在Rt△PDM中,(x+5)2=(10-x)2+25,
∴x=![]() ,
,
∴AM=![]() ,
,
设EB=EM=m,
在Rt△AEM中,则有m2=(10-m)2+(![]() )2,
)2,
∴m=![]() ,
,
∴AE=10-![]() ,
,
∵AM⊥EF,
∴∠ABM+∠GEF=90°,∠GEF+∠EFG=90°,
∴∠ABM=∠EFG,
∵FG=BC=AB,∠A=∠FGE=90°,
∴△BAM≌△FGE(AAS),
∴EG=AM=![]() ,
,
∴CF=BG=AB-AE-EG=10-![]() .
.