题目内容
【题目】综合与实践
问题情境
数学活动课上,老师让同学们根据如下问题情境,发现并提出问题.
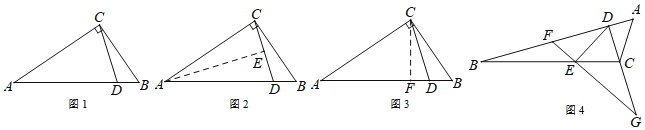
如图1,△ABC与△EDC都是等腰直角三角形,点E,D分别在AC和BC上,连接EB.将线段EB绕点B顺时针旋转90°,得到的对应线段为BF.连接DF.“兴趣小组”提出了如下两个问题:①AE=BD,AE⊥BD;②DF=AB,DF⊥AB.
解决问题:
(1)请你证明“兴趣小组”提出的第②个问题.
探索发现:
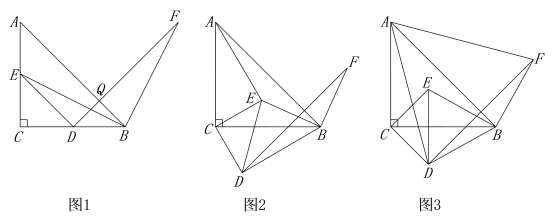
(2)“实践小组”在图1的基础上,将△EDC绕点C顺时针旋转角度![]() (0°<
(0°<![]() <90°),其它条件保持不变,得到图2.
<90°),其它条件保持不变,得到图2.
①请你帮助“实践小组”探索:“兴趣小组”提出的两个问题是否还成立?如果成立,请给出证明;若不成立,请说明理由.
②如图3,当AD=AF时,请求出此时旋转角α的大小.
【答案】(1)见解析;(2)①成立,见解析;②45°
【解析】
(1)根据等腰直角三角形的性质及线段的和差关系可得AE=DB,由旋转的性质可得∠EBF=90°,BE=BF,根据三角形外角性质及角的和差关系可得∠AEB=∠DBF,利用SAS可证明△AEB≌△DBF,可得AB=DF,∠ABE=∠DFB,由∠ABE+∠ABF=90°可得∠DFB+∠ABF=90°,即可得出∠AQF=90°,可得AB⊥DF;
(2)①如图,延长AE与BD交于点P,交BC于O,根据旋转的性质可得∠ACE=∠DCB,利用SAS可证明△ACE≌△BCD,可得AE=BD,∠CAE=∠CBD,根据角的和差关系可得∠APB=90°,可得AE⊥BD;根据三角形外角性质及角的和差关系可得∠AEB=∠DBF,利用SAS可证明△AEB≌△DBF,可得AB=DF,∠ABE=∠DFB,由∠ABE+∠ABF=90°可得∠DFB+∠ABF=90°,即可得出∠AQF=90°,可得AB⊥DF;
②根据AD=AF,AB⊥DF可得AB垂直平分DF,可得BD=BF=BE,利用SSS可证明△BEC≌△BDC,可得∠DCB=∠ECB=![]() ∠ECD=45°,根据旋转的性质可得α=∠DCB=45°.
∠ECD=45°,根据旋转的性质可得α=∠DCB=45°.
(1)∵△ABC与△EDC为等腰直角三角形,
∴AC=BC,EC=DC,
∴AE=DB.
∵将线段EB绕点B顺时针旋转90°,得到的对应线段为BF,
∴∠EBF=90°,BE=BF,
∵∠AEB=∠C+∠EBC,∠DBF=∠EBF+∠DBE,∠C=∠EBF=90°,
∴∠AEB=∠DBF.
在△AEB和△DBF中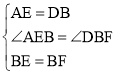 ,
,
∴△AEB≌△DBF,
∴AB=DF,∠ABE=∠DFB.
∵∠ABE+∠ABF=90°,
∴∠DFB+∠ABF=90°,
∴∠AQF=90°,即AB⊥DF.
(2)①如图,延长AE与BD交于点P,交BC于O,
∵将△EDC绕点C顺时针旋转角度![]()
∴∠ACE=∠DCB,
在△ACE和△BCD中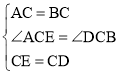 ,
,
∴△ACE≌△BCD,
∴AE=BD,∠CAE=∠CBD.
∵∠AOC=∠BOP,∠AOC+∠CAO=90°,
∴∠CBD+∠BOP=90°,
∴∠APB=90°,即AP⊥BD.
∵∠AEB=∠APB+∠EBD,∠DBF=∠EBF+∠DBE,∠APB=∠EBF=90°,
∴∠AEB=∠DBF.
在△AEB和△DBF中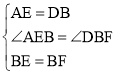 ,
,
∴△AEB≌△DBF,
∴AB=DF,∠ABE=∠DFB.
∵∠ABE+∠ABF=90°,
∴∠DFB+∠ABF=90°,
∴∠AQF=90°,即AB⊥DF.
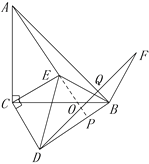
②∵AD=AF,AB⊥DF,
∴AB垂直平分DF.
∴BD=BF=BE,
在△BEC和△BDC中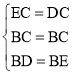 ,
,
∴△BEC≌△BDC,
∴∠DCB=∠ECB=![]() ∠ECD=45°.
∠ECD=45°.
∴旋转角α的大小是45°.

 习题精选系列答案
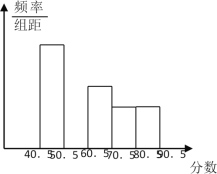
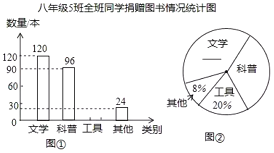
习题精选系列答案【题目】丁老师为了解所任教的两个班的学生数学学习情况,对数学进行了一次测试,获得了两个班的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.①A、B两班学生(两个班的人数相同)数学成绩不完整的频数分布直方图如下(数据分成 5 组:x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
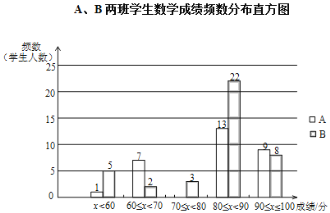
②A、B两班学生测试成绩在80≤x<90这一组的数据如下:
A 班:80 80 82 83 85 85 86 87 87 87 88 89 89
B 班:80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
③A、B两班学生测试成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
A班 | 80.6 | m | 96.9 |
B班 | 80.8 | n | 153.3 |
根据以上信息,请写出表中 m、n的值____________.