题目内容
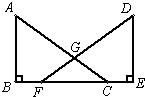 22、已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE.求证:(1)△ABC≌△DEF;(2)GF=GC.
22、已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE.求证:(1)△ABC≌△DEF;(2)GF=GC.分析:(1)要证△ABC≌△DEF,可根据SAS判定.
(2)由△ABC≌△DEF可证∠ACB=∠DFE,即证GF=GC.
(2)由△ABC≌△DEF可证∠ACB=∠DFE,即证GF=GC.
解答:证明:(1)∵BF=CE,
∴BF+FC=CE+FC,即BC=EF.
又∵AB⊥BE,DE⊥BE,
∴∠B=∠E=90°.
又∵AB=DE,
∴△ABC≌△DEF.
(2)∵△ABC≌△DEF,
∴∠ACB=∠DFE.
∴GF=GC.
∴BF+FC=CE+FC,即BC=EF.
又∵AB⊥BE,DE⊥BE,
∴∠B=∠E=90°.
又∵AB=DE,
∴△ABC≌△DEF.
(2)∵△ABC≌△DEF,
∴∠ACB=∠DFE.
∴GF=GC.
点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,本题是一道较为简单的题目.

练习册系列答案
相关题目
 20、已知:如图,点O为?ABCD的对角线BD的中点,直线EF经过点O,分别交BA、DC的延长线于点E、F,求证:AE=CF.
20、已知:如图,点O为?ABCD的对角线BD的中点,直线EF经过点O,分别交BA、DC的延长线于点E、F,求证:AE=CF. OA上一动点(与点O、A不重合).EF⊥AB于点F,交y轴于点G.设点E的横坐标为x,△BGF的面积为y.
OA上一动点(与点O、A不重合).EF⊥AB于点F,交y轴于点G.设点E的横坐标为x,△BGF的面积为y. 已知:如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.BF,CE相交于点O.
已知:如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.BF,CE相交于点O.
 (2013•淮阴区模拟)已知:如图,点E、A、C在同一条直线上,AB=CE,AC=CD,BC=ED.求证:AB∥CD.
(2013•淮阴区模拟)已知:如图,点E、A、C在同一条直线上,AB=CE,AC=CD,BC=ED.求证:AB∥CD.