题目内容

已知：如图，点P是半径为5cm的⊙O外的一点，OP=13cm，PT切⊙O于T，过P点作⊙O的割线PAB，（PB＞PA）．设PA=x，PB=y，求y关于x的函数解析式，并确定自变量x的取值范围．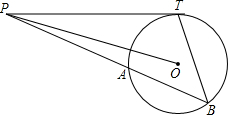

分析：连接OT，根据切线的性质定理和勾股定理求得PT的长，再根据切割线定理建立函数关系式，最后由圆外一点到圆的最大距离和最小距离确定x的取值范围．

解答：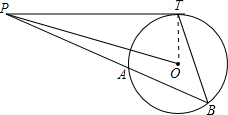

解：连接OT，得直角三角形OPT；
∵OP=13cm，OT=5cm，
∴PT=12cm，
∵PT²=PA•PB，
∴y=

144

x

（8≤x＜12）．

点评：综合运用了切线的性质定理、勾股定理和切割线定理．注意：过圆外一点和圆心作直线和圆相交于点M，N，则PM即是它的最小值，PN即是它的最大值．

练习册系列答案

暑假生活上海教育出版社系列答案

暑假天地重庆出版社系列答案

暑假作业非常5加2白山出版社系列答案

学力水平快乐假期系列答案

独占鳌头暑假乐园河北人民出版社系列答案

新思维新捷径新假期暑假新捷径吉林大学出版社系列答案

寒假作业内蒙古教育出版社系列答案

桃李文化快乐暑假武汉出版社系列答案

优秀生快乐假期每一天全新寒假作业本系列答案

假日英语暑假吉林出版集团股份有限公司系列答案

相关题目

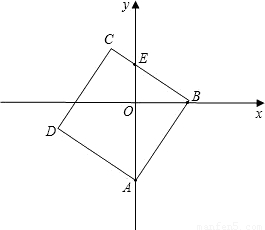
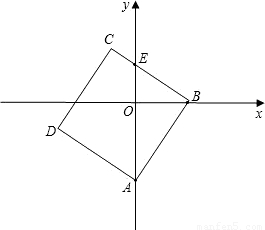
已知：如图，点O是平面直角坐标系的原点，点A的坐标为（0，-4），点B为x轴上一动点，以线段AB为边作正方形ABCD（按逆时针方向标记），正方形ABCD随着点B的运动而随之相应变动．点E为y轴的正半轴与正方形A

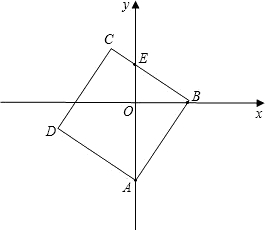BCD某一边的交点，设点B的坐标为（t，0），线段OE的长度为m．
（1）当t=3时，求点C的坐标；
（2）当t＞0时，求m与t之间的函数关系式；
（3）是否存在t，使点M（-2，2）落在正方形ABCD的边上？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．

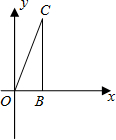（2012•鄂州）已知，如图，△OBC中是直角三角形，OB与x轴正半轴重合，∠OBC=90°，且OB=1，BC=

，将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍，使OB₁=OC，得到△OB₁C₁，将△OB₁C₁绕原点O逆时针旋转60°再将其各边扩大为原来的m倍，使OB₂=OC₁，得到△OB₂C₂，…，如此继续下去，得到△OB₂₀₁₂C₂₀₁₂，则m=

．点C₂₀₁₂的坐标是

（-2²⁰¹³，0）

（-2²⁰¹³，0）

已知：如图，点O是平面直角坐标系的原点，点A的坐标为（0，-4），点B为x轴上一动点，以线段AB为边作正方形ABCD（按逆时针方向标记），正方形ABCD随着点B的运动而随之相应变动．点E为y轴的正半轴与正方形ABCD某一边的交点，设点B的坐标为（t，0），线段OE的长度为m．
（1）当t=3时，求点C的坐标；
（2）当t＞0时，求m与t之间的函数关系式；
（3）是否存在t，使点M（-2，2）落在正方形ABCD的边上？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．

已知：如图，点O是平面直角坐标系的原点，点A的坐标为（0，-4），点B为x轴上一动点，以线段AB为边作正方形ABCD（按逆时针方向标记），正方形ABCD随着点B的运动而随之相应变动．点E为y轴的正半轴与正方形ABCD某一边的交点，设点B的坐标为（t，0），线段OE的长度为m．
（1）当t=3时，求点C的坐标；
（2）当t＞0时，求m与t之间的函数关系式；
（3）是否存在t，使点M（-2，2）落在正方形ABCD的边上？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．

（2013•惠山区一模）已知：如图，点O是平面直角坐标系的原点，点A的坐标为（0，-4），点B为x轴上一动点，以线段AB为边作正方形ABCD（按逆时针方向标记），正方形ABCD随着点B的运动而随之相应变动．点E为y轴的正半轴与正方形ABCD某一边的交点，设点B的坐标为（t，0），线段OE的长度为m．
（1）当t=3时，求点C的坐标；
（2）当t＞0时，求m与t之间的函数关系式；
（3）是否存在t，使点M（-2，2）落在正方形ABCD的边上？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．