题目内容
已知:如图,点A、B分别在x轴、y轴上,以OA为直径的⊙P交AB于点C(-| 2 |
| 5 |
| 4 |
| 5 |
 OA上一动点(与点O、A不重合).EF⊥AB于点F,交y轴于点G.设点E的横坐标为x,△BGF的面积为y.
OA上一动点(与点O、A不重合).EF⊥AB于点F,交y轴于点G.设点E的横坐标为x,△BGF的面积为y.(1)求直线AB的解析式;
(2)求y与x之间的函数关系式,并写出自变量x的取值范围.
分析:(1)如图,过C作CM⊥OA于M,CN⊥OB于N,则CM=
,CN=
,根据已知可以知道OM=CN,然后证明△ACM∽△COM,利用对应边成比例可以求出AM,然后求出A的坐标,再利用待定系数法可以求出直线AB的解析式;
(2)如图依题意得到OE=-x,根据已知可以证明△GEO∽△GBF∽△ABO,然后利用它们对应边成比例,分别表示BF,GF,最后表示△BGF的面积.
| 4 |
| 5 |
| 2 |
| 5 |
(2)如图依题意得到OE=-x,根据已知可以证明△GEO∽△GBF∽△ABO,然后利用它们对应边成比例,分别表示BF,GF,最后表示△BGF的面积.
解答: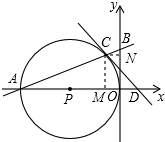 解:(1)如图:
解:(1)如图:
过C作CM⊥OA于M,CN⊥OB于N,则CM=
,CN=
.
根据相交弦定理,得CM2=OM•AM,
∵OM=CN,
∴AM=
,
∴OA=OM+AM=
+
=2.
∴A(-2,0).
设直线AB的解析式为y=kx+b,
把A,C两点坐标代入,得
,
∴k=
,b=1,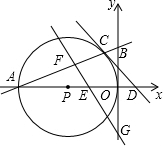
∴直线AB的解析式为y=
x+1;
(2)∵AB的解析式为y=
x+1,
∴当x=0时,y=1,
∴OB=1,
∴tan∠BAO=
=
,
而∠BAO+∠ABO=90°,∠FGB+∠FBG=90°,
∴∠BAO=∠FGB,
∴tan∠FGB=
,
∴sin∠FGB=
,cos∠FGB=
,而E(x,0),
∴OE=-x,
∴OG=-2x,
∴BG=1-
x,
∴根据三角函数可知,GF=BG•cos∠FGB,BF=BG•sin∠FGB,
∴y=
•BF•GF=(1-
x)2.
 解:(1)如图:
解:(1)如图:过C作CM⊥OA于M,CN⊥OB于N,则CM=
| 4 |
| 5 |
| 2 |
| 5 |
根据相交弦定理,得CM2=OM•AM,
∵OM=CN,
∴AM=
| 8 |
| 5 |
∴OA=OM+AM=
| 2 |
| 5 |
| 8 |
| 5 |
∴A(-2,0).
设直线AB的解析式为y=kx+b,
把A,C两点坐标代入,得
|
∴k=
| 1 |
| 2 |

∴直线AB的解析式为y=
| 1 |
| 2 |
(2)∵AB的解析式为y=
| 1 |
| 2 |
∴当x=0时,y=1,
∴OB=1,
∴tan∠BAO=
| OB |
| OA |
| 1 |
| 2 |
而∠BAO+∠ABO=90°,∠FGB+∠FBG=90°,
∴∠BAO=∠FGB,
∴tan∠FGB=
| 1 |
| 2 |
∴sin∠FGB=
2
| ||
| 5 |
| ||
| 5 |
∴OE=-x,
∴OG=-2x,
∴BG=1-
| 3 |
| 2 |
∴根据三角函数可知,GF=BG•cos∠FGB,BF=BG•sin∠FGB,
∴y=
| 1 |
| 2 |
| 3 |
| 2 |
点评:把三角函数,待定系数法,相似三角形的性质与判定都结合在一起,综合性比较强.

练习册系列答案
相关题目
 20、已知:如图,点O为?ABCD的对角线BD的中点,直线EF经过点O,分别交BA、DC的延长线于点E、F,求证:AE=CF.
20、已知:如图,点O为?ABCD的对角线BD的中点,直线EF经过点O,分别交BA、DC的延长线于点E、F,求证:AE=CF. 已知:如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.BF,CE相交于点O.
已知:如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.BF,CE相交于点O.
 (2013•淮阴区模拟)已知:如图,点E、A、C在同一条直线上,AB=CE,AC=CD,BC=ED.求证:AB∥CD.
(2013•淮阴区模拟)已知:如图,点E、A、C在同一条直线上,AB=CE,AC=CD,BC=ED.求证:AB∥CD.