题目内容
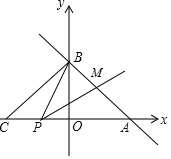
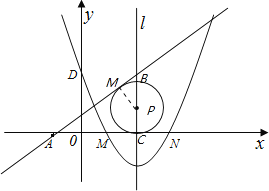
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),直线l是抛物线的对称轴.
(1)求该抛物线的解析式.
(2)若过点A(﹣1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,求此直线的解析式.
(3)点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,求点P的坐标.
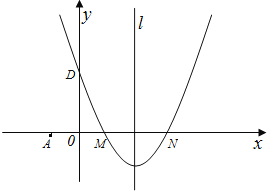
【答案】解:(1)∵抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),
∴假设二次函数解析式为:y=a(x﹣1)(x﹣3),
将D(0,3),代入y=a(x﹣1)(x﹣3),得:
3=3a,
∴a=1,
∴抛物线的解析式为:y=(x﹣1)(x﹣3)=x2﹣4x+3;
(2)∵过点A(﹣1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,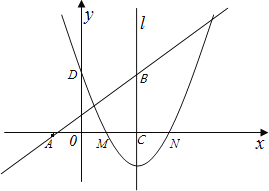
∴![]() AC×BC=6,
AC×BC=6,
∵抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,
∴二次函数对称轴为x=2,
∴AC=3,
∴BC=4,
∴B点坐标为:(2,4),
一次函数解析式为;y=kx+b,
∴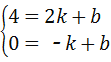 ,
,
解得:![]() ,
,
y=![]() x+
x+![]() ;
;
(3)∵当点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,
∴MO⊥AB,AM=AC,PM=PC,
∵AC=1+2=3,BC=4,
∴AB=5,AM=3,
∴BM=2,
∵∠MBP=∠ABC,
∠BMP=∠ACB,
∴△ABC∽△CBM,
∴![]() ,
,
∴![]() ,
,
∴PC=1.5,
P点坐标为:(2,1.5).
【解析】略

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目