题目内容
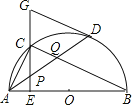
【题目】如图，四边形ABCD是正方形，动点E、F分别从D、C两点同时出发，以相同的速度分别在边DC、CB上移动，当点E运动到点C时都停止运动，DF与AE相交于点P，若AD=8，则点P运动的路径长为（ ）
A. 8
B. 4 C. 4π D. 2π
【答案】D
【解析】
如图，连接AC、BD交于点O．首先证明∠DPE=∠APD=90°，即可推出点P的运动轨迹是以AD为直径的圆上的弧OD，由此即可解决问题.
解：如图，连接AC、BD交于点O．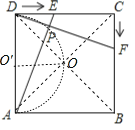
∵DE=CF，AD=DC，∠ADE=∠DCF，
∴△ADE≌△DCF，
∴∠DAE=∠CDF，
∵∠DAE+∠AED=90°，
∴∠CDF+∠DEP=90°，
∴∠DPE=∠APD=90°，
∴点P的运动轨迹是以AD为直径的圆上的弧OD，
∴点P运动的路径长为
2π4=2π，
故选：D
练习册系列答案
阅读快车系列答案
相关题目
